Vincent Auvray - Contributions (Back)

Quick insight of the transparent motion estimation

Three main approaches are proposed in the litterature to estimate transparent motions:

Partial adaptation of classical motion estimators (Black and Anandan, Irani and Peleg), but for partial transparencies only.

Detection of planes in the 3D Fourier space (Shizawa and Mase, Pingault and Pellerin, Stuke and Aach), but it must assume that motions are translationals over dozen of frames.

Transparent motion estimation in the direct space (Pingault and Pellerin, Stuke and Aach, Toro), which relies on an equation equivalent for the brightness consistancy. For two layers:



It assumes that the motions are constant over two successive time intervals.

Our contributions in bitransparent configuration

In a first time, we have developed a synthetic image generation process which follows the physics of X-Ray image formation. That allows us to compare our estimates to a known ground truth. (More)

We have developped three generations of motion estimators dedicated to the bitransparency. This refers to a transparency made of two layers over the image. (And two layers only!)

Our first contribution (presented to ICIP'05) did not allow us to reach an estimation accuracy good enough on clinical sequences with a realistic noise.

This is why we imagined a second algorithm, presented at MICCAI'05. To be as robust to noise as possible, we tried to constraint the problem as much as we could. Many real exams observations convinced us that the anatomical motions (heart beating, lungs dilation, diaphragm translation) could be modeled with affine displacement fields.
This approach allows for precisions of 0.6 and 2.8 pixels on images typical for diagnostic and interventional images respectively.

We finally proposed in ICIP'06 an evolution of this algorithm, reaching precisions of 0.6 pixels on diagnostic images and 1.2 on fluoroscopic images, and presented real examples.

Estimated motion fields on a part of cardiac exam in situation of bi-transparency.

Our contributions in bidistributed transparency

Our contributions until that point estimated the transparent motions present in a sequence showing one configuration only: two layers having coherent motions were present over the whole image. Most of the contributions on this topic refer to this situation.
Now, the real images are more complex: they contain more than two layers overall, but rarely more than two locally. Which is why we have introduced the concept of bidistributed transparency to account for images that can be segmented in areas containing one or two layers.
We present in ICIP'06 a joint transparent motion estimation and segmentation method that allows for precions of 0.6 pixels on diagnostic images and 1.2 on fluoroscopic images.(More)

Two images for a fluoroscopic sequence, the estimated motions (the field corresponding to the background is worth zero and thus invisible) and the resulting segmentation.

Processing of a video sequence in a situation of bi-distributed transparency. Top left: the segmentation in layers, top right the estimated motions, and on the bottom the compensated difference images.

We also present a demo, showing the different stages of motion estimation.

Application to denoising

We also need to know how to use this motion information to denoise our sequences. We have proposed an original framework to do so in MICCAI'05.
. It yielded a very disappointing asymptotic deoising of 20%. (More)

We have therefore developed the so-called hybrid filters, which decide locally between different possible motion compensations:

Transparent motion compensation when both layers are textured.

Compensation of the motion of the more textured layer in any other case (one layer only is textured, or both layers are homogeneous). This way, we preserve the useful information without impairing the achievable denoising power.

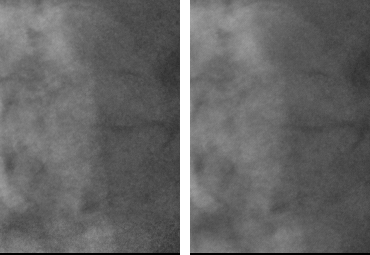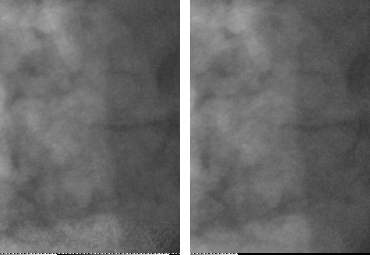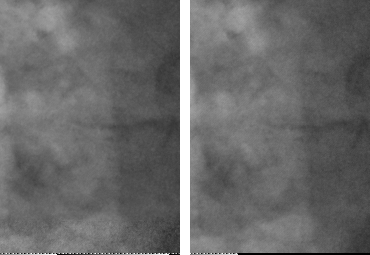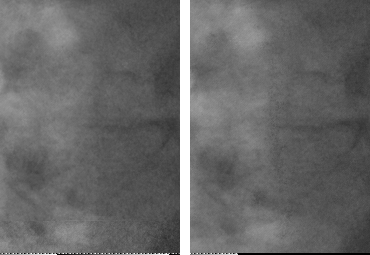Fluoroscopic sequence processing with the temporal hybrid filter (left) and a classical adaptative temporal filter (right). The heart is much more contrasted on the left for an equivalent denoising.

Retour