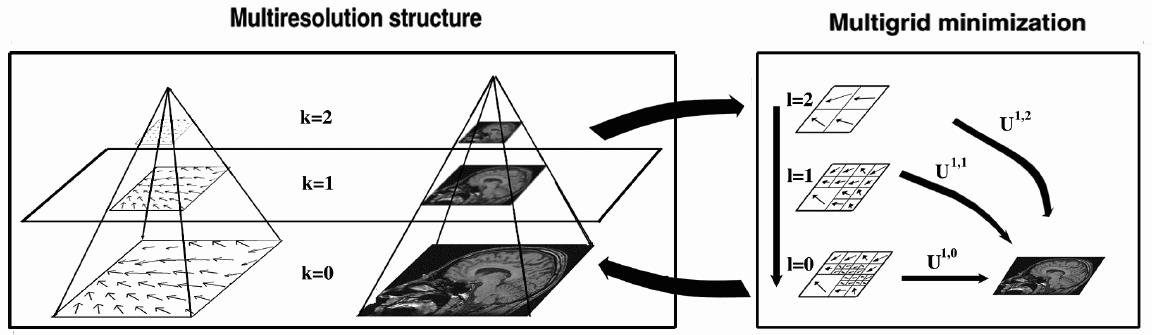
Example of multiresolution/multigrid minimization. For each resolution
level (on the left), a multigrid strategy (on the right) is performed.
For clarity reasons, the figure is a 2D illustration of a 3D algorithm
with volumetric data.
| Multimodality registration |
Contact: Pierre Hellier , Christian Barillot
| Context |
Nowadays functional activity of the brain can be observed by different ways. Among all the modalities (SPECT, PET, fMRI, EEG, MEG), fMRI (functional MRI) appears to be an appealing technique because it offers a good compromise between spatial and temporal resolution and because of its reduced cost. To exploit these images, fMRI acquisitions must be merged with anatomical images such as T1-MRI, which means that a multimodal registration must be performed.
When the volumes are acquired from the same patient, only a rigid (translations+rotations) transformation is estimated to register the different data. However, fMRI acquisitions (EPI) can introduce geometrical distortions that can only be compensated by a non-linear registration process. The deformations might reach up to several millimeters, causing large errors in the localization of the functional activity.
| Method |
For rigid multimodal registration, several techniques have been proposed. Among them, volumetric methods based on the maximization of a similarity measure have proved to give good results. In particular, mutual information (Wells et al, Maes et al) and correlation ration (Roche et al) are the most popular similarity measures.
To perform multimodal non-linear registration, we extended the work explained here to the multimodal case. We compute the deformation field by minimizing a cost function including two terms: a similarity measure (in this case the mutual information) and a regularization term (quadratic difference of the deformation field between neighbors). At each grid level, we use the Powell algorithm to minimize the cost function. The following figure presents an illustration of the multigrid minimization:

Example of multiresolution/multigrid minimization. For each resolution
level (on the left), a multigrid strategy (on the right) is performed.
For clarity reasons, the figure is a 2D illustration of a 3D algorithm
with volumetric data.
| Results |
Results of the registration of the deformed T2 with the anatomical T1 are shown on the next figure. The T1 is displayed with grey colormap, whereas the registered T2 is mapped onto the T1 with a different colormap. After a rigid registration process, the local non-linear deformations induced by the thin plate can be seen in the mid-plane area (on the coronal view), as well as in the ventricles structures (on the axial view).
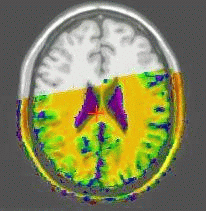
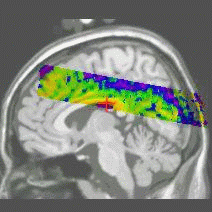
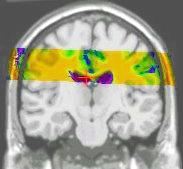
results of the rigid registration
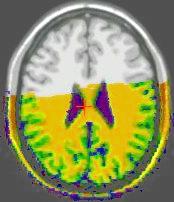
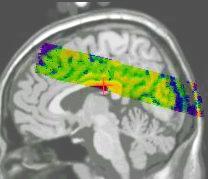
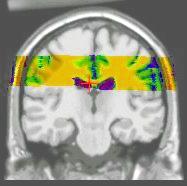
results of the non-linear multigrid registration
| References |
| This work is currently under review. |
| Webmaster : vista_webmaster@irisa.fr
Last modified: Wed Feb 2 10:24:54 MET 2000 |