



Next: Performance Evaluation of the
Up: New LM with Adaptive
Previous: New LM with Adaptive
Contents
Index
The Algorithm with Adaptive Momentum
The goal is to choose minimization directions, which are not interfering and linearly independent. This can be achieved by the selection of conjugate directions which forms the basis of the CG method. Two vectors are non-interfering and linearly or mutually conjugate with respect to
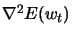 when
when
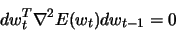 |
(1025) |
where
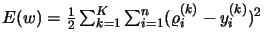 ,
,
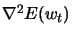 is the Hessian matrix
is the Hessian matrix
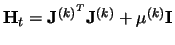 , with
, with 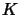 is the number of training patterns,
is the number of training patterns, 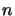 is the number of outputs,
is the number of outputs, 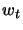 the weights vector, and
the weights vector, and 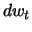 is the optimal step (or the search direction). The objective is to reach a minimum of the cost function with respect to
is the optimal step (or the search direction). The objective is to reach a minimum of the cost function with respect to 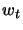 and to simultaneously maximize
and to simultaneously maximize
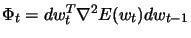 without compromising the need for a decrease of the cost function. At each iteration of the learning process, the weight vector
without compromising the need for a decrease of the cost function. At each iteration of the learning process, the weight vector 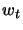 will be incremented by
will be incremented by 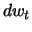 , so that:
, so that:
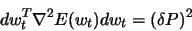 |
(1026) |
where 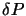 is a constant and the change
is a constant and the change 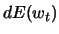 in
in 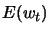 is equal to a predetermined quantity
is equal to a predetermined quantity
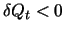 :
:
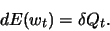 |
(1027) |
This is a constrained optimization problem which can be analytically solved by introducing two Lagrange multipliers 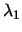 and
and 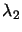 . Then function
. Then function 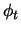 is introduced to evaluate the differentials involved in the right hand side and to substitute the function
is introduced to evaluate the differentials involved in the right hand side and to substitute the function 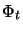 :
:
![\begin{displaymath}
\phi _t =\Phi _t + \lambda _1 (\delta Q_t -dE(w_t)) +\lambda _2 [(\delta P)^2 -dw_t^T \nabla ^2 E(w_t) dw_t].
\end{displaymath}](img512.gif) |
(1028) |
By replacing 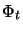 by its value, we obtain:
by its value, we obtain:
![\begin{displaymath}
\phi _t = dw_t ^T\nabla ^2 E(w_t)dw_{t-1} +\lambda_1 (\de...
...w_t) +\lambda_2[(\delta P)^2 -dw_t^T \nabla ^2 E(w_t) dw_t].
\end{displaymath}](img513.gif) |
(1029) |
To maximize 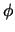 at each iteration, the following equations must be satisfied:
at each iteration, the following equations must be satisfied:
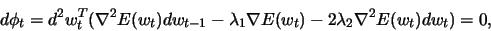 |
(1030) |
and
![\begin{displaymath}
d^2 \phi_t =-2\lambda_2[d^2w_t^T\nabla^2E(w_t)d^2w_t] < 0.
\end{displaymath}](img516.gif) |
(1031) |
Hence from 10.30 we obtain:
![\begin{displaymath}
dw_t =-\frac{\lambda_1}{2\lambda_2}[\nabla^2 E(w_t)]^{-1}\nabla E(w_t)+\frac{1}{2\lambda_2} dw_{t-1}.
\end{displaymath}](img517.gif) |
(1032) |
From equations 10.27 and 10.32 we obtain:
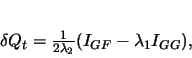 |
(1033) |
where
![\begin{displaymath}
I_{GG}=\nabla E(w_t)^T [\nabla^2 E(w_t)]^{-1}\nabla E(w_t),
\end{displaymath}](img519.gif) |
(1034) |
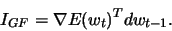 |
(1035) |
From 10.33 we obtain 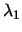 :
:
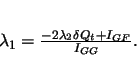 |
(1036) |
It remains to obtain 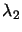 . This can be done by substituting Eqn. 10.30 in Eqn. 10.26 to obtain:
. This can be done by substituting Eqn. 10.30 in Eqn. 10.26 to obtain:
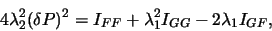 |
(1037) |
where
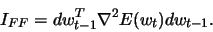 |
(1038) |
Finally, Eqn. 10.36 is substituted into Eqn. 10.37 and solve for 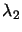 to obtain:
to obtain:
![\begin{displaymath}
\lambda_2=\textstyle \frac{1}{2} \displaystyle \left [
...
...{I_{FF}I_{GG}-I_{GF}^2}
\right]^{-\textstyle \frac{1}{2}}.
\end{displaymath}](img524.gif) |
(1039) |
The positive square root value has been chosen for 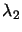 in order to satisfy Eqn. 10.31. Note the bound
in order to satisfy Eqn. 10.31. Note the bound
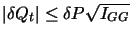 set on the value of
set on the value of 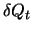 by Eqn. 10.39. The value chosen for
by Eqn. 10.39. The value chosen for 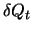 is always:
is always:
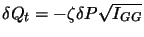 where
where 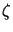 is a constant between 0 and 1. Therefore the free parameters are
is a constant between 0 and 1. Therefore the free parameters are 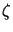 and
and 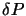 (
(
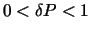 ). The authors recorded during their simulations that the best results are given for
). The authors recorded during their simulations that the best results are given for
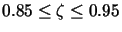 and
and
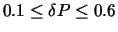 .
.




Next: Performance Evaluation of the
Up: New LM with Adaptive
Previous: New LM with Adaptive
Contents
Index
Samir Mohamed
2003-01-08