Benoît Caillaud
Synet is a software package synthesizing bounded Petri-nets, based on the algorithms described in [1,3,4,2]. It also comprizes a new synthesis algorithm based on the computation of extremal rays of polyhedral cones.
A PDF version of this document is also available.
The package contains several executables and a library:
A couple of utilities are also provided:
The Synet package has been first developped in 1996 and 1997 by Benoît Caillaud and Eric Badouel at IRISA, Rennes, France. It has been improved in 1999 by Benoît Caillaud, with the implementation of a new synthesis algorithm based on the computation of extremal rays of polyhedral cones.
The current version of the tool should be considered as a preliminary prototype rather than a stable and robust tool. Therefore it is not freely available and researchers that are willing to use this tool should contact the author (Benoit.Caillaud@irisa.fr).
The software requires :
SYNET is known to compile correctly on Sparc/Solaris and Intel-486/Linux systems. However it should compile correctly on most POSIX compliant systems. A port to Windows NT is under way.
Two environment variables must be defined:
If the default make command is GNU-make:
[balta]bc: make
Otherwise:
[balta]bc: gmake
[balta]bc: cp synet psynet ocamlsynet distribute \
reachability draw_aut draw_net $BINDIR
Where $BINDIR is the directory where the executables are to be placed.
synet [<options>] <.aut-file-name> synet [<options>] -l <.aut-file-name> synet [<options>] -d <.dis-file-name> <.aut-file-name> synet [<options>] -r [-d <.dis-file-name>] <.aut-file-name>
Where:
<.aut-file-name> is a filename of an Open/Caesar .aut
transition graph.
<.dis-file-name> is a filename of a distribution of actions.
All other possible options are:
Usage: synet { <options> } <filename>
where <options> ::= <option> { <options> }
<option> ::= -d <filename>
| -l
| -n
| -i
| -p
| -x
| -o <filename>
| -v <integer>
| -q
| -e <filename>
| -w
| -r
| -c <filename>
| -z <filename>
.dis format.
-c.
The symbol (a)means that the option is not yet implemented. (b)indicates that this option is assumed by default.
Terminal symbols <nat>, <string> and <ident> respectively
represent natural integers, character strings and identifiers in OCaml syntax.
<state-id> ::= <nat> | <string> | <ident> <event-id> ::= <nat> | <string> | <ident> <location-id> ::= <nat> | <string> | <ident> <place-id> ::= <nat> | <string> | <ident>
This file format extends the .aut format of Open/Caesar[5]
and Aldebaran.
<.aut> ::= des(<nat>,<nat>,<nat>) <trans-list> <trans-list> ::= | <trans> <trans-list> <trans> ::= ( <state-id> , <event-id> , <state-id> )
Because of a bug in aldebaran that has never been corrected, users are strongly advised to declare initial state as state 0.
<.dis> ::= <mapping-list> <mapping-list> ::= | <mapping> <mapping-list> <mapping> ::= ( <event-id> , <location-id> )
Every event of the automaton must have a unique mapping.
<.cut> ::= <essp-list> <essp-list> ::= | <essp> <essp-list> <essp> ::= ( <state-id> , <event-id> )
Every event-state separation problem (essp) must be an essp of the automaton.
<.net> ::= <statement-list>
<statement-list> ::= | <statement> <statement-list>
<statement> ::= <location> | <transition> | <place> | <flow>
<location> ::= location <location-id>
<transition> ::= transition <event-id> {:: <location-id>}
<place> ::= place <place-id> {:= <nat>} {:: <location-id>}
<flow> ::= flow <place-id> -- { <nat> | # } -> <event-id>
| flow <place-id> <- { <nat> } -- <event-id>
Flow arcs of the form flow p - # -> t are inhibitor arcs. They are generated by the distribute command.
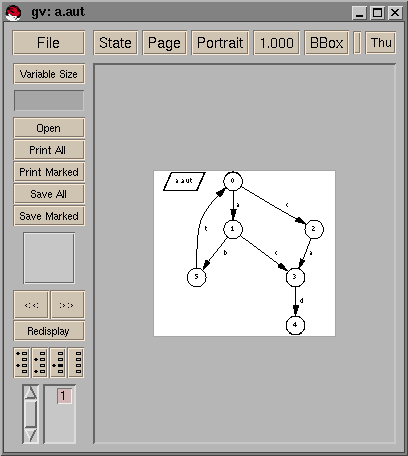
File a.aut defines in the Aldebaran syntax a simple but easy to
understand automaton:
des(0,7,6) (0,a,1) (0,c,2) (1,b,5) (1,c,3) (2,a,3) (3,d,4) (5,t,0)
File a.dis contains a location mapping of the events of automaton
a.aut over two processes: A and B.
(a,A) (b,B) (c,B) (d,A) (t,A)
SYNET produces the following output:
localhost[1]% synet -r -o a.net -d a.dis a.aut The transition system is separated. Synthesized net: +a-d-t::A +c-d::A -a+t:=1::A +b-t::A +a-b::B -c-b+t:=1::B localhost[2]%
An the Petri net is saved in file a.net:
location B location A transition t :: A transition d :: A transition b :: B transition c :: B transition a :: A place x_5 := 1 :: B place x_4 :: B place x_3 :: A place x_2 := 1 :: A place x_1 :: A place x_0 :: A flow x_5 ---> b flow x_5 ---> c flow x_4 ---> b flow x_3 ---> t flow x_2 ---> a flow x_1 ---> d flow x_0 ---> t flow x_0 ---> d flow x_5 <--- t flow x_4 <--- a flow x_3 <--- b flow x_2 <--- t flow x_1 <--- c flow x_0 <--- a
Both the automaton and the Petri can be visualized:
localhost[3]% draw_aut a.aut --- a.aut --- localhost[4]% draw_net a.net localhost[5]%
The command draw_aut displays the following window:

And draw_net displays:
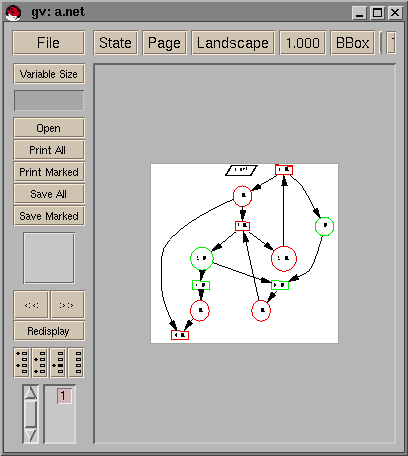
The synthesized Petri-net can be directly visualized:
synet -r -x -d a.dis a.aut.
This section details an application of distributable Petri net synthesis. A correct by construction implementation of a simple transport level communication protocol, the INRES protocol [6], is synthesized using the algorithms presented in the previous sections. For the sake of clarity, the method is first detailed on a simplified version of the protocol, and then applied on the full protocol, however with an increased complexity. The example illustrates a new methodology for distributed program synthesis, based on the algorithms for distributable Petri net synthesis presented briefly in the previous sections and in greater details in [2].
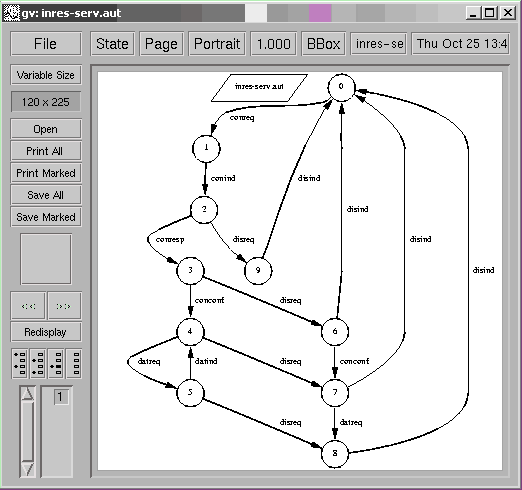
In this section, we consider a simplified version of the INRES communication protocol [6]. The specification of service of the INRES protocol is given below:
localhost[6]% draw_aut inres-serv.aut
For the sake of the exposition, we consider the simplified service described below:
localhost[7]% cat prot.dis (s,A) (r,B) (d,B) (a,A) localhost[8]% draw_aut prot.aut
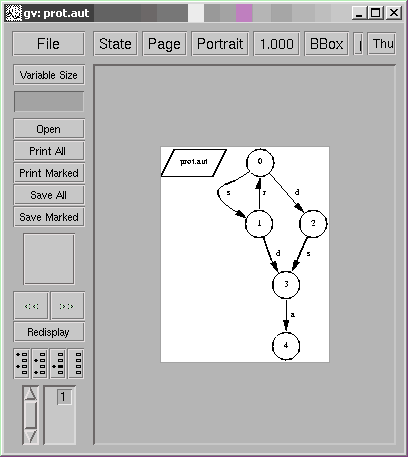
The simplified protocol defines the transmission of data between two users user-A and user-B linked to respective protocol entities A and B. Event s means that entity A is given by user-A some data to transmit; event r means that entity B delivers some data to user-B; event d is a disconnection request (located on B); event a is the notification of the disconnection (located on A). With this protocol, data exchanges (words in (sr)*) may take place until a disconnection is requested.
We aim at synthesizing a distributed implementation of this protocol: two processes A and B, communicating with one another through a reliable communication medium. Events s and a are located on process A, while events r and d are located on B. This is defined by the location map l: l(s)=l(a)=A and l(r)=l(d)=B.
We wish to use distributable Petri net synthesis to produce a Petri net implementation of the communication protocol: thus, for every place p of the net, the flow relation F must satisfy: F(p,s)=F(p,a)=0 or F(p,r)=F(p,d)=0.
Unfortunately the automaton specifying the service (shown above) is not isomorphic to the marking graph of any distributable Petri net: event a and state 2 cannot be separated, as it is shown below:
localhost[9]% synet -x -r -d prot.dis prot.aut Event-state separation failures: Event a and state 2 are not separated. Synthesized net: -s+r:=1::A +d-a::A +a::A +s-r::B -d/r:=1::B
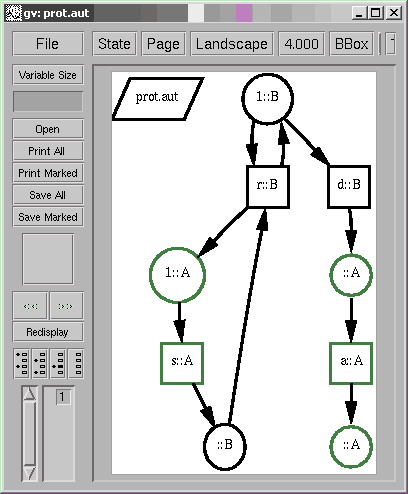
However this can be alleviated by refining the automaton into a weakly bisimilar automaton which is actually the marking graph of a distribuable Petri net. In [7], is advocated an event splitting heuristics for refining non separated automata into separated automata. In our case, the two occurrences of s may be replaced by s1 and s2, and similarly for d, leading to three different refinements. However, none of the refined automata is separated with respect to the restricted set of localizable regions, compatible with the distribution constraints. Even though in the non distributed case event splitting is a systematic method for refining automata into separated automata, it is potentially useless in the distributed case.
As an alternative resort, refinement can be done by inserting silent transitions while keeping weak bisimilarity. In our case, the adequate refinement step consists in replacing transition (3,a,4) by two transitions: (3,t,4) and (4,a,5) (see the automaton below), with silent event t located on process B.
localhost[10]% cat prot_r.dis (s,A) (r,B) (d,B) (a,A) (t,B) localhost[11]% draw_aut prot_r.aut
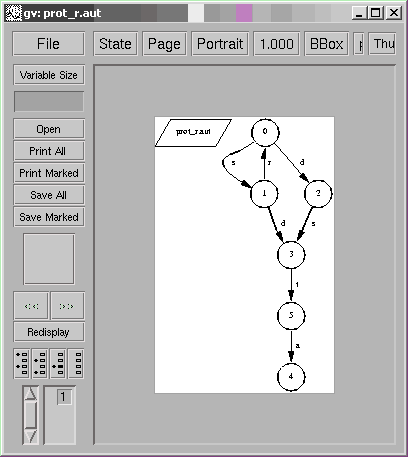
The refined automaton is then isomorphic to the reachable marking graph of the Petri net shown below. Places and transitions are sorted according to their locations: A on the left and B on the right.
localhost[12]% synet -x -r -d prot_r.dis prot_r.aut The transition system is separated. Synthesized net: -s+r:=1::A +t-a::A +s-r-t::B +d-t::B -d/r:=1::B
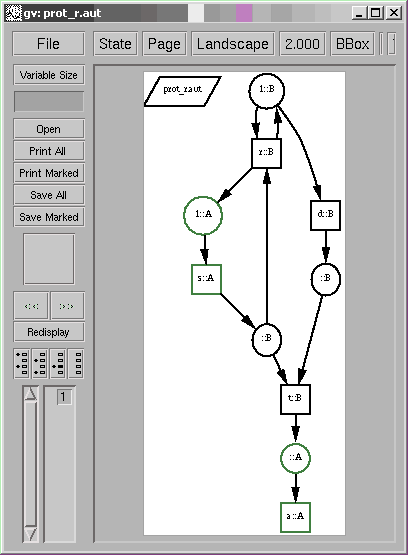
The distributable Petri net is then expanded into the Petri net shown below by making communications between processes explicit:
localhost[13]% distribute prot_r.net prot_rd.net localhost[14]% draw_net prot_rd.net
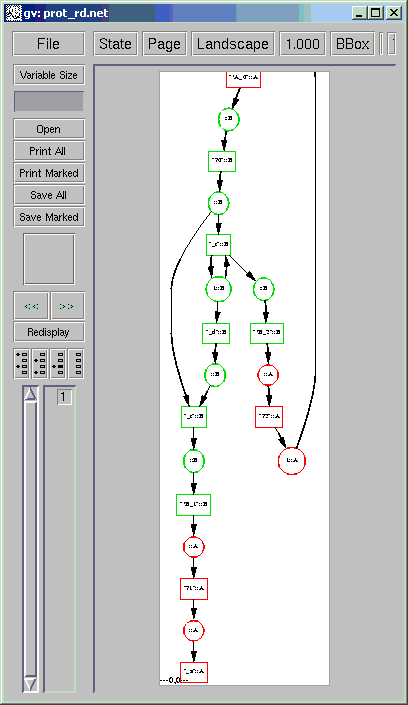
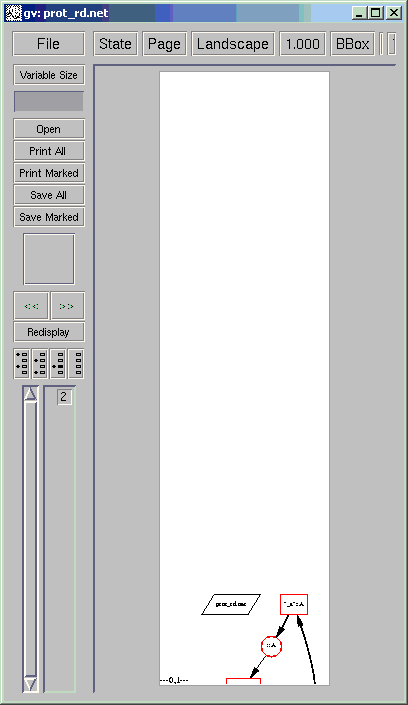
By distributing its reachable state graph as indicated in [2], with an abstraction from event t and with minimization, one obtains the automata shown below:
localhost[13]% draw_aut prot_rd_A.aut localhost[14]% draw_net prot_rd_B.aut
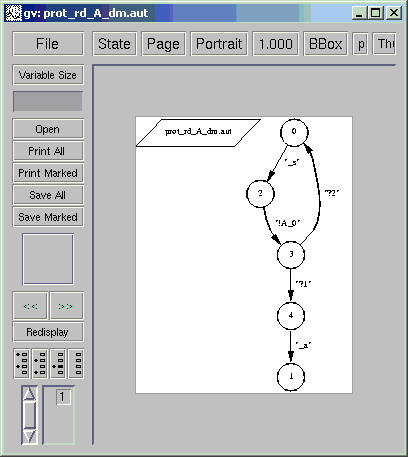
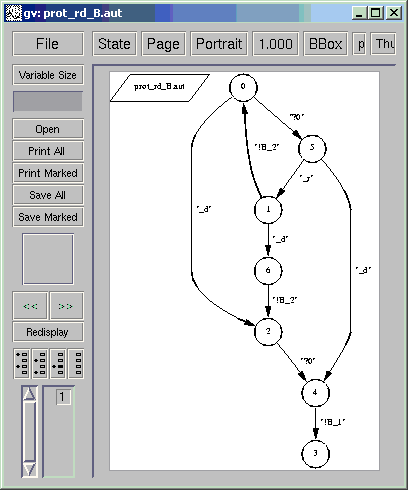
It follows from the method that this distributed implementation is behaviorally correct.
As in the previous section, the same method can be used to deal with the full INRES protocol, however with an increased complexity. The protocol to be realized consists in two processes A and B communicating through an asynchronous communication network. The automaton below gives the expected behaviour (specification of service) of the distributed protocol:
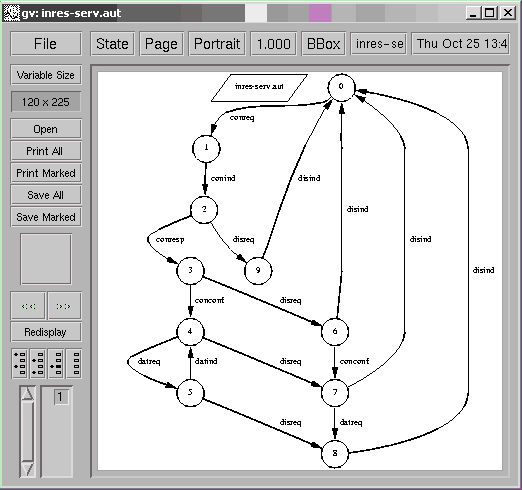
Events Conreq, Conconf, Datreq and Disind are located on process A, while events Conind, Disreq, Conresp and Datind are located on process B.
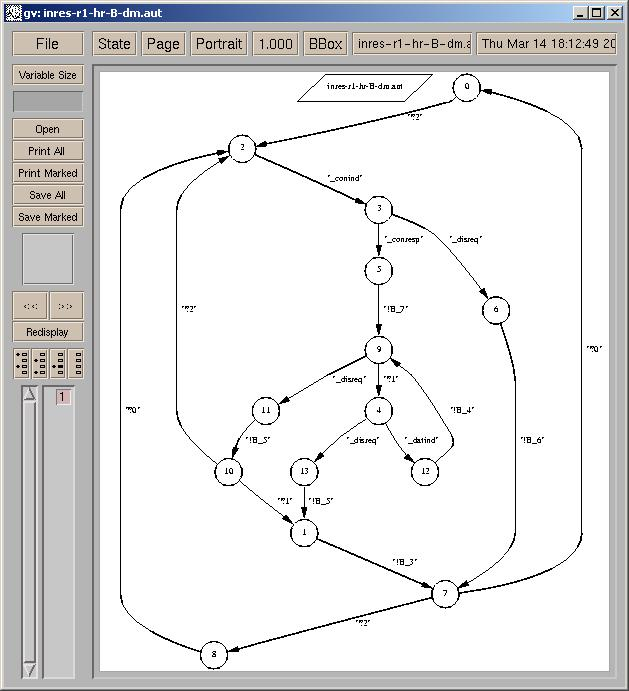
It should be noticed that the specification of service of the INRES protocol is not co-deterministic : there are three transitions labelled Disind entering the initial state. However, splitting the occurrences of Disind is not sufficient to secure realizability in a distributed Petri net. A further refinement step has to take place : The specification should be refined into an equivalent one modulo weak bisimulation, shown below. This is done by both event splitting and insertion of a silent transition. Finding the proper location of insertion of the silent transition is guided by intuition solely. In this latter automaton, events Conreq, Conconf, Datreq and Disind1 through Disind4 are located on A ; events Conind, Disreq1, Disreq2, Conresp, Datind and t are located on B.
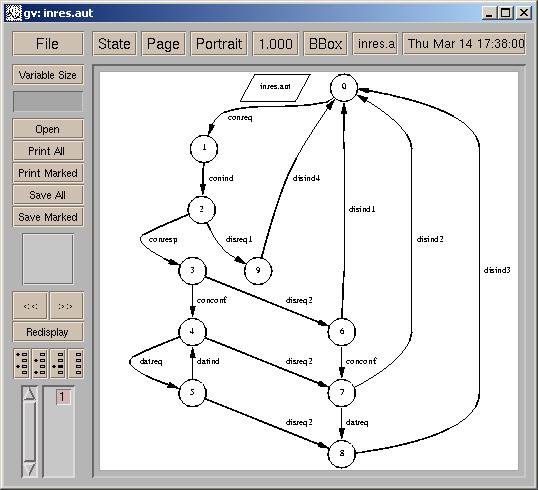
The automaton is realized in the distributable Petri net shown below:
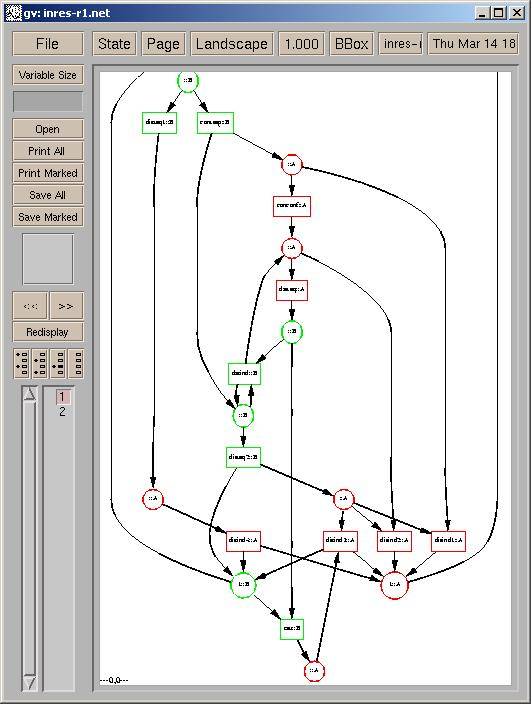
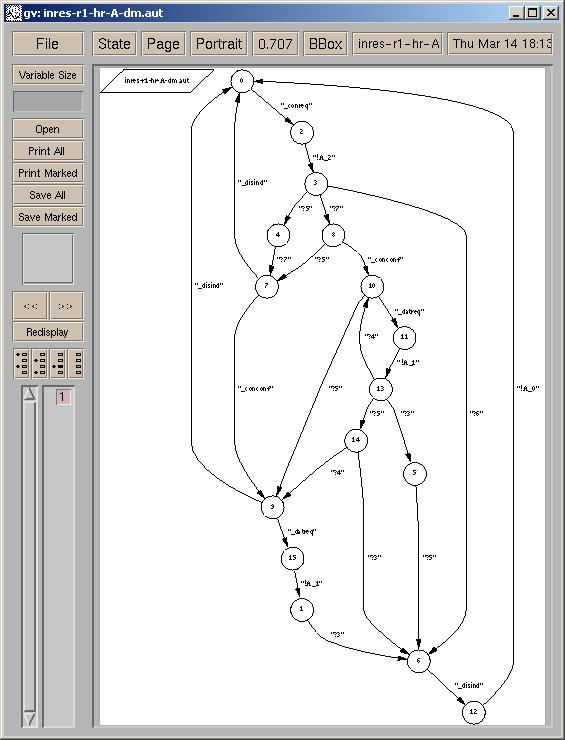
This Petri net yields the communicating automata given below, a correct by construction implementation of the INRES service:
This document was generated using the LaTeX2HTML translator Version 99.2beta8 (1.43)
Copyright © 1993, 1994, 1995, 1996,
Nikos Drakos,
Computer Based Learning Unit, University of Leeds.
Copyright © 1997, 1998, 1999,
Ross Moore,
Mathematics Department, Macquarie University, Sydney.
The command line arguments were:
latex2html -split 0 synet
The translation was initiated by Benoit Caillaud on 2002-03-15