Positioning a camera parallel to an unmarked plane

Description of the demonstration

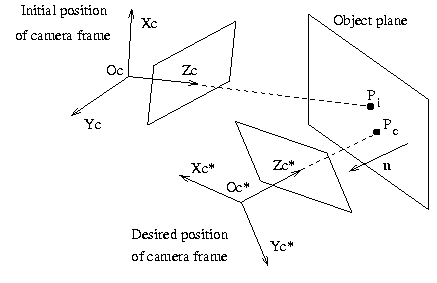
The aim of this robotic task is to control an eye-in-hand system in order to position the projection plane of a camera (or image plane) parallel to an observed plane (or object plane). This plane is unmarked, which means that no geometric visual features, such as points or straight lines, can be easily extracted. Furthermore, a second task is joined to the first one so that the same point is always observed at the image center, to ensure the scene stays viewable.

These two joined tasks are achieved as following:

• Orientation of the optical axis parallel to the normal of the plane (which is equivalent to have the image and observed planes parallel) is performed by controlling the pan and tilt d.o.f. of the camera. This is done by regulating to zero the quadratic parameters of motion in the image, under the constraint of a constant translational motion along the optical axis.

• Fixation, meaning keeping the same point at the image center, is done by controlling the translational d.o.f. perpendicular to the optical axis. Two ways have been studied:

  • Keeping a null speed at the image center by direct compensation of displacement due to rotation.

  • Estimating the position of the initial image center by integration of its speed along time and regulating this position to zero.

The task is sum up on the following figure where P_i and P_c represents the initial and desired 3D point of the object projected at the image center. The fixation task control the system in order to have P_i = P_c.

Expected result of the task

Results

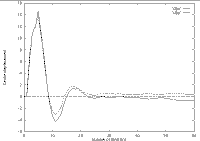
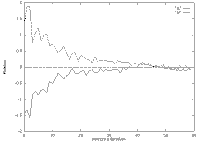
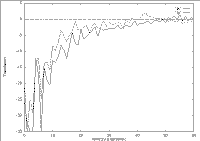
The results presented underneath have been obtained on our 6 d.o.f. Cartesian robot. A typical initial scene used is first displayed, then are successively presented:

• the quadratic parameters on which is based the control of rotational d.o.f.

• the estimated displacement of the initial image center by integration of its 2D speed and which is regulated by the translational d.o.f.

• the computed rotational speeds sent to the robot

• the computed translational speeds

• the estimated angular error. This error is computed using an a priori orientation of the reference plane, which is of course unused in the control loop.

(Click on results curves to see them bigger)

Initial scene

Regulated quadratic parameters	Estimated displacement of initial center
Controlled rotational speeds	Controlled translational speeds

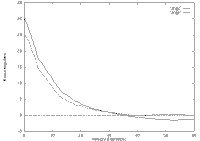Angular errors

Collaborations

This work is included in project VIDAC (Dynamic Active VIsion and Communication), itself part of the XI^th plan contract Brittany Council - French State driven in collaboration with TIPA team at Cemagref(in French only) and TEMICS at IRISA.

References

1. A.Crétual, F. Chaumette. Positioning a camera parallel to a plane using dynamic visual servoing - IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS'97), pp 43-49, Grenoble, France, September 1997