Cooperation between local and global approaches to register brain images

Contact: Pierre Hellier , Christian Barillot

Purposes

We have investigated here the introduction of cortical constraints for non rigid inter-subject brain registration. We extract sulcal patterns with the active ribbon method (LINK). An energy based registration method (LINK) makes it possible to incorporate the matching of cortical sulci, and express in a unified framework the local sparse similarity and the global ``iconic'' similarity.

Method

Computation of the sparse constraint

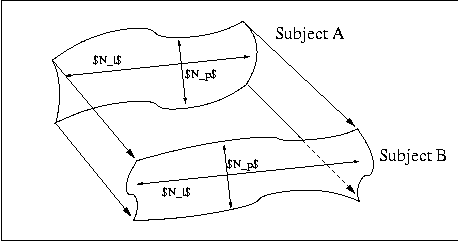
Extracted cortical sulci are modeled with B-splines, which facilitates their numerical manipulation. In particular, the resampling of these shapes is possible on each axis. For the registration of a subject A towards a subject B, we consider the homologous sulci between these two subjects. For each pair of homologous sulci, the sulcus containing with fewer control points is resampled so that the two homologous sulci are finally described by the same number of points. Then, we explicitly put in correspondence the control points of these two sulci. This is summarized on next figure. We have also designed a matching procedure that copes with the interruption of cortical sulci.

Complete energy-based framework

The sparse deformation field wc, deduced from the matching of cortical ribbons, must be integrated in the formulation of the registration problem. We incorporate that information as a third energy term, which is a similarity between the estimated field and the sparse constraint. The cost function thus becomes:

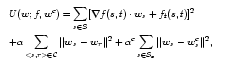
The matching of cortical ribbons, as presented in the past section, might not be correct for all the points of the ribbons. As a matter of fact, there might be some segmentation errors, and these points should not be used as a hard constraint. Furthermore, we do not really know if it is anatomically correct to assume a one-to-one correspondence between the sulci. Therefore, we
introduce a robust estimator on the cortical constraint term.

The local cortical constraint will have a relative spatial influence for two reasons. On the one hand, the standard regularization term propagates the local constraint because the minimization is alternated. One the other hand, the multigrid minimization, described in details in our previous work makes it possible to estimate a deformation model on specified cubes, which will propagate the local constraint to a large group of voxels that compose the cube.

Results

Once every subject of the database has been mapped into the reference subject, it is possible to compute an average volume, by normalizing the 17 deformed volumes. Note that all the volumes are computed with the estimated deformation field and trilinear interpolation. The results are presented below, with axial, sagittal and coronal views for both methods. Looking at cortical areas, we can see that the average volume is less blurred and more similar to the reference volume. On other regions, the results are identical.


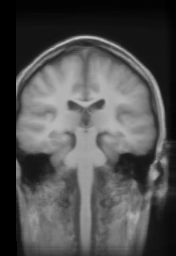
Average volume without constraint

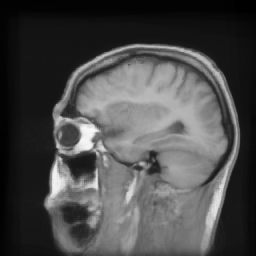
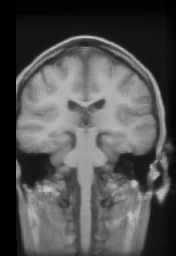
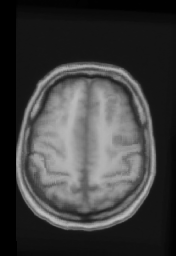
Average volume with cortical constraint

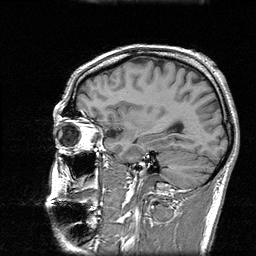
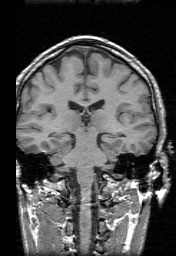
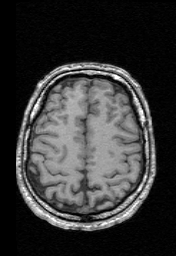
Reference volume

If we consider one particular sulcus over the database of $18$ subjects, one can deform each sulcus with the estimated deformation field and look at the superposition with the reference sulcus. The visualization for the central left sulcusis shown below. One can observe the variability of the registered sulci with the previous method, and the way sulci are registered with the modified method. This is, however, not surprising, since this information has been explicitely included in the registration process.



References

  1. P. Hellier, C. Barillot. Cooperation between local and global approaches to register brain images. Proc. Information processing in Medical Imaging, IPMI, M.-F. Insana, R.-M. Leahy (eds.), Lecture Notes in Computer Science 2082, pages 315-328, Davis, USA, Juin 2001.
Webmaster : vista_webmaster@irisa.fr
Last modified: Wed Feb 2 10:24:54 MET 2000