

Contact: Romeo Tatsambon Fomena
Creation Date: February 2007
Visual servoing is exploited to move an eye-in-hand system to a position where the desired pattern of the image of the target can be observed. The camera is a paracatadioptric system which consists in the coupling of a parabolic mirror with an orthographic camera. The target is 4 cm radius polystyrene white ball. Using such simple object allows to easily compute the selected visual features on the observed disk (image of the ball) at video rate without any image processing prolem. The desired features have been computed after moving the robot to a position corresponding to the desired image. The following figures picture the desired (left) and initial (right) images used for each experiment.

 |
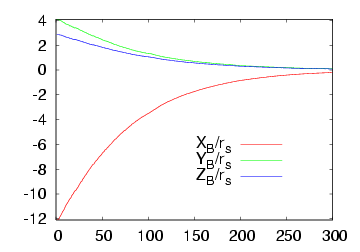
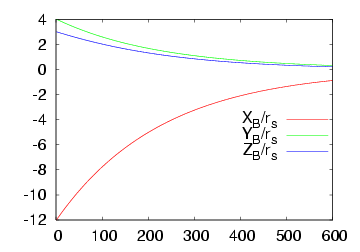
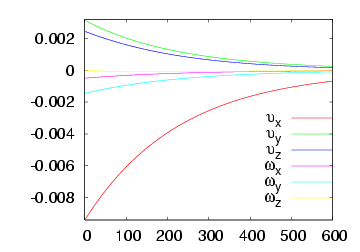
Here we consider the case where the value of the radius of the ball is available. The following figures describe the system behaviour: the figure on the left pictures the trajectory of the visual features error while the figure on the right plots the camera velocities. The video for this case is available here
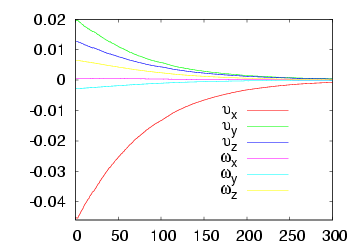 |
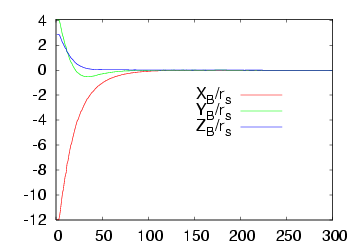
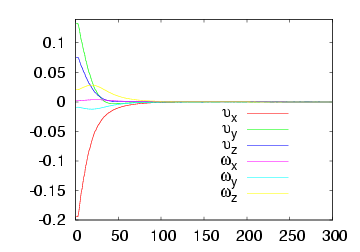
In practice, the value of the radius of the ball is unknown. However, visual servoing still converges: this result has been proved in theory. Here we propose two experiments to validate this proof. We first consider an over approximation of the radius of the ball: R = 20 cm that is 5 times the real radius. The system behaviour is plotted below on the first row. We can note a fast convergence of the system. In the second case, we suppose an under approximation of the radius of the ball: R = 0.8 cm that is 1/5 times the real radius. The figures on the second row below describe the system behaviour. We can observe a slow convergence. This slow or fast convergence of the system is due to the fact that the value of R acts like a gain. The behaviour of the system could be easily improved by using an adaptive gain.
 |
 |
This work is concerned with modeling issues in visual servoing. The challenge is to find optimal visual features for visual servoing. The optimality criteria being: local and -as far as possible- global stability of the system, robustness to calibration and to modeling errors, none singularity nor local minima, satisfactory trajectory of the system and of the measures in the image, and finally linear link and maximal decoupling between the visual features and the degrees of freedom taken into account.
A spherical projection model is proposed to search for optimal visual features. Compared to the perspective or omnidirectional projection models, determining optimal features with this projection model is quite easy and intuitive. Using this projection model, a new optimal set of visual features has been designed for visual servoing from spheres with any central catadioptric system. Using this new combination, a classical control law has been proved to be globally stable to modeling error: in practice, it means that, is not necessary to use the real radius of the sphere target; a rough estimate is sufficient.
|
| Lagadic
| Map
| Team
| Publications
| Demonstrations
|
Irisa - Inria - Copyright 2009 © Lagadic Project |