Visual Servoing Based on Dynamic Vision

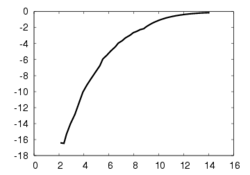Contact : Christophe Collewet

Creation Date : March 2007

Context

Visual servoing is a widely used technique in robot control. However, synthesizing the control law requires usually a model of the scene observed by the camera and also the knowledge of the desired features. We consider here the cases when this knowledge is not available. Let us cite for example applications in the surgical domain, agriculture, agrifood industry or in unknown environments like underwater or space. This problem can also appear when considering specific tasks, like perception tasks, where the camera has to move w.r.t. an object of interest to perform automatically an optical character recognition task. In that case, the desired image is also unknown since the goal of the task is precisely to move the camera to see clearly the characters to decode.

Overview

This demo page shows how to control the camera orientation with respect to the tangent plane at a certain object point corresponding to the center of a region of interest and to observe this point at the principal point to fulfill a fixation task. A 3D reconstruction phase has thus to be performed during the camera motion. Our approach is then close to the structure-from-motion problem. The reconstruction phase is based on the measurement of the 2D motion in a region of interest and on the measurement of the camera velocity. Since the 2D motion depends on the shape of objects being observed, a unified motion model is introduced to cope as well with planar as with non-planar objects. However, since this model is only an approximation, two approaches are proposed to enlarge its domain of validity. The former is based on active vision, coupled with a 3D reconstruction based on a continuous approach, while the latter is based on statistical techniques of robust estimation, coupled with a 3D reconstruction based on a discrete approach.

Experimental results

Using active vision

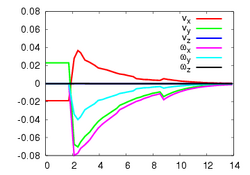
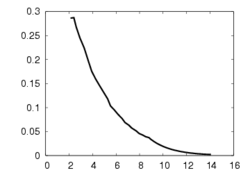
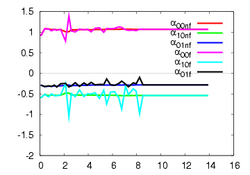
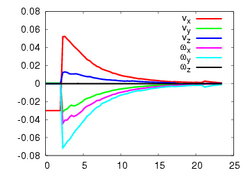
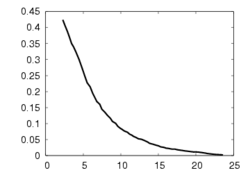
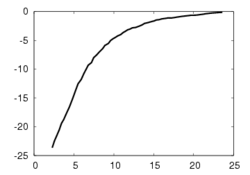
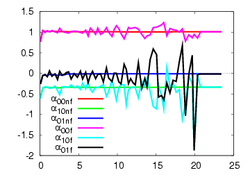
This experiment concerns a cylinder of radius 7 cm and consists in positioning the camera so that the desired orientation of the tangent plane at a certain point is (15°, 0°) around the x and y axes respectively (the z axis beeing carried out by the optical axis). Fig. 1a depicts the components of the camera velocity (m/s or rad./s); Fig. 1b the norm of the task function to achieve the task; Fig. 1c the magnitude of the rotation to reach the desired orientation (deg.); Fig. 1d the behavior of some parameters related to the tangent plane (filtered and non-filtered) expressed in a fixed frame. The initial and final images are reported respectively on Fig. 1e-f. First, the figures 1a and 1b confirm that the control law converges without any problem. The final orientation of the tangent plane w.r.t. the camera was (14.2°, 1.9°) while the initial orientation was (-1.5°, -4.8°, 4.7°). Consequently, we obtain an accurate positioning. Note that without using active vision a bad result is obtained since we have (13.0°, 3.0°).

(a) (b)

(c) (d)

(e) (f)

Figure 1: first experiment - use of active vision.

A second experiment concerns a more realistic scene, the goal is to perform a perception task (see Fig. 2 where the first and the last images are represented). A video of this experiment is available. Here is what the camera is seeing and here , the trajectory of the camera.

(a) (b)

Figure 2: second experiment - use of active vision.

Using robust estimation

The first experiment concerns a sphere of radius 7 cm and consists in positioning the camera parallel to the tangent plane at a certain point. Fig. 3 depicts the same paremeters as in Fig. 1. Here again, the control law converges without any problem. The initial orientation was (-17°, -17.2°, -1.9°) and the final orientation was (0.4°, 0.4°). Without using robust estimation, a higher orientation error has been obtained since we had (-4.8°, 2.8°).

(a) (b)

(c) (d)

(e) (f)

Figure 3: first experiment - use of robust estimation.

A second experiment concerning a perception task has been performed (see Fig. 3). A video of this experiment is available. Here , what the camera is seeing and here , the trajectory of the camera.

(a) (b)

Figure 4: second experiment - use of robust estimation.

Comparison between both approaches

Using active vision usually leads to good results. Nevertheless, when the curvature of the object and the desired orientation are high, we have seen that a poor accuracy could be obtained. In addition, since the computation of the 2D motion dedicated to this approach is not time consuming, active vision is used with a 3D reconstruction based on a continuous approach. It allows to recover the structure from a linear system with an optimal condition number. Consequently, it provides less noisy results than the use of robust estimation.

On the other hand, using a selection of points is very time consuming, this approach leads to a low acquisition rate (around 400 ms) and requires therefore a discrete approach to be really effective. Thus, the 3D reconstruction is performed through the resolution of a non-linear system and provides consequently more noisy results than a continuous approach like active vision. In addition, with a low acquisition rate, only slow camera motion can be considered. It can be seen as the main drawback of this approach. Conversely, the computation cost of using active vision is low (around 280 ms) and thus higher 3D velocities can be reached. However, selecting points has led to better results than active vision under hard conditions (high curvature and desired orientation).

References

1. C. Collewet, F. Chaumette. Visual Servoing on Non-Planar Objects From Active Vision, IEEE Int. Conf. on Robotics and Automation, ICRA'07, Rome, Italy, Avril 2007.
2. C. Collewet, F. Chaumette. Using Robust Estimation for Visual Servoing Based on Dynamic Vision, IEEE Int. Conf. on Robotics and Automation, ICRA'07, Rome, Italy, Avril 2007.