Proper Orthogonal Decomposition (back)

Description

We propose a method to enhance the estimation of the temporal modes in a Proper Orthogonal Decomposition (POD).

POD is a technique that allows to represent the motion of fluid flows as a linear combination of modes obtained through a a singular value decomposition of the temporal correlation matrix of a set of experimental measurements. These measurements are usually obtained through Particle Image Velocimetry (PIV) methods applied on a large set of pairs of images showing the flow of interest.
The modes explaining the largest part of the kinetic energy are kept to represent the spatio-temporal motion field.
A Galerkin projection of the Navier Stokes equation on this set of modes enables to construct a Low Order Dynamical Syatem (LODS) representing the flow. Such a system is constituted by a set of Ordinary Differential Equations(ODE).

The coefficients of the ODE are usually computed by applying a least square regression on the PIV data. Different realizations of the fluid flow can then be synthetised given different intial conditions.

However, when the PIV observations are noisy, the estimation of the ODE coefficients are very inacurate and may lead to completly erroneous simulation.

In this work, we have proposed a technique relying on data assimilation that allows to improve the ODE's coefficients estimation. This approach consists in solving a system gathering noisy measurements of the ODE coefficient given by POD and a noisy version of the LODS.
This comes to estimate the minimizer of a spatio-temporal functional. The optimization is processed through an adjoint technique. .

Results

Experience 1: flow behind a static cylinder

6 temporal modes on 1000 images

 

Estimation	Assimilation

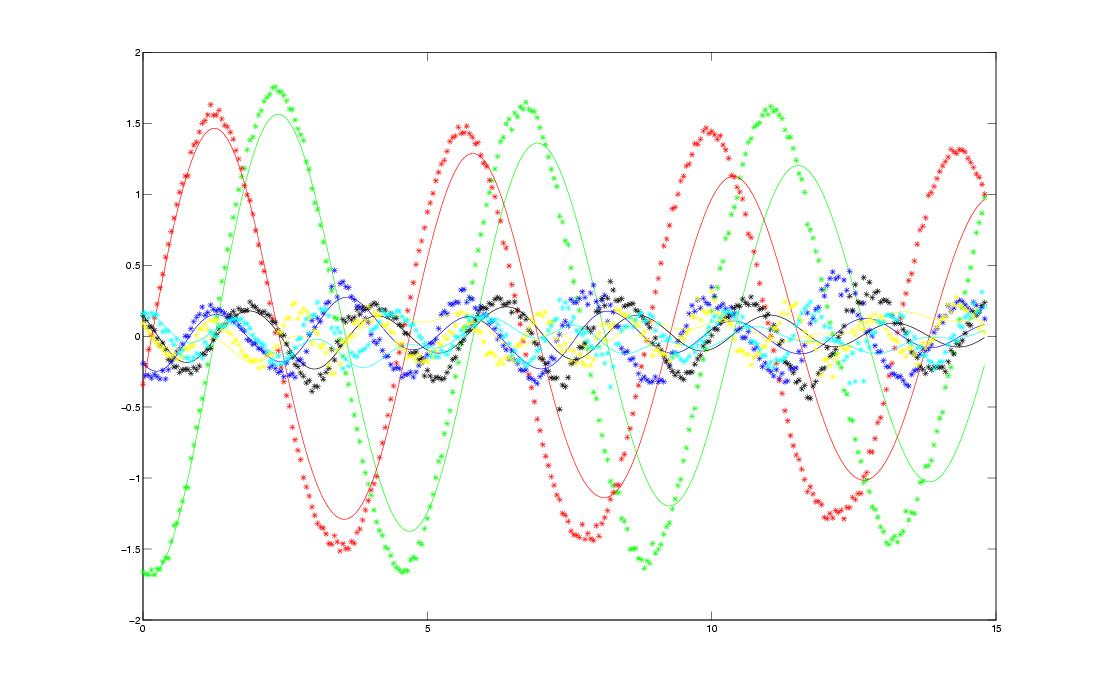
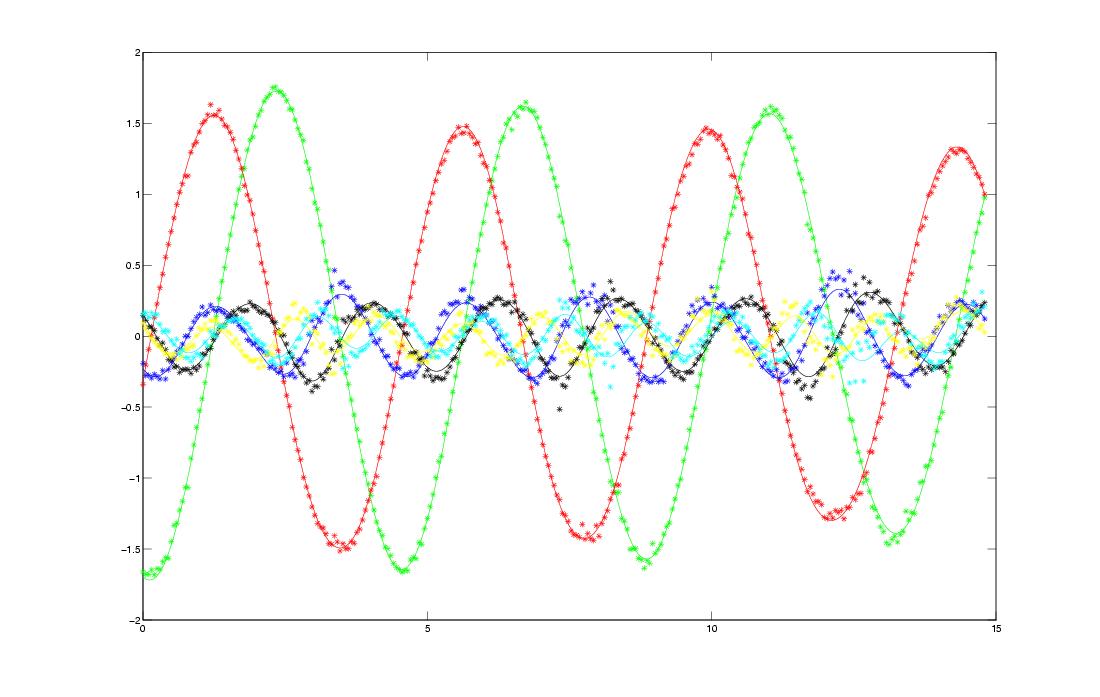
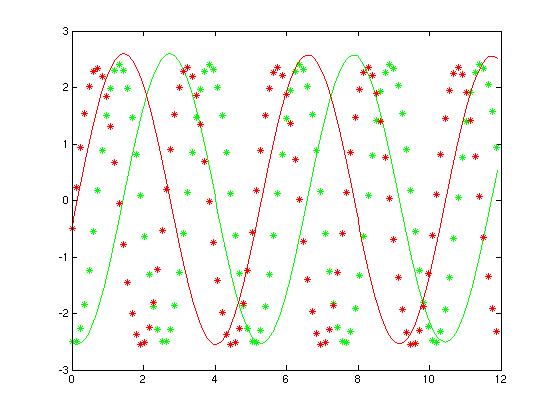
The PIV observations are represented by plots * . The estimation is developped from the initial condition with the coefficients computed by a least square approximation of the PIV data. The assimilation uses this first estimation and converges on the observations.

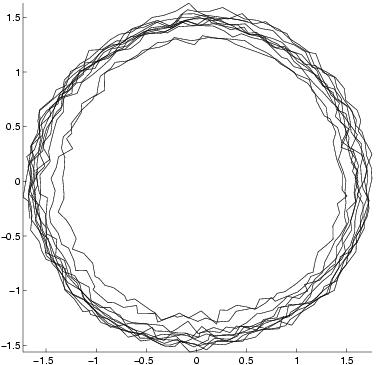
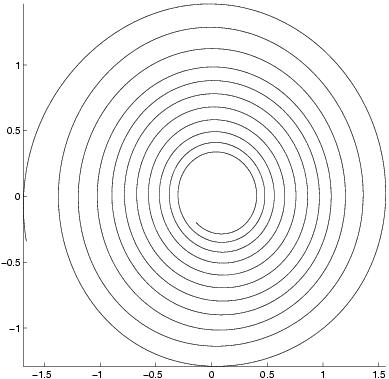
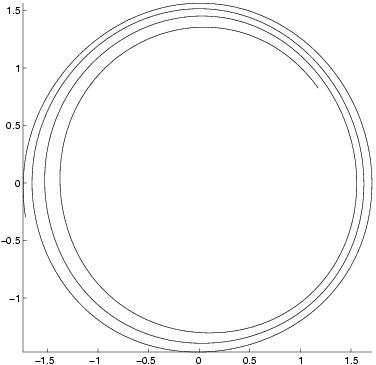
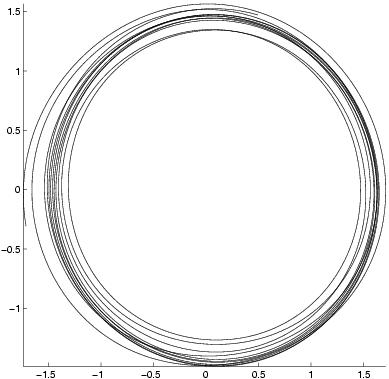
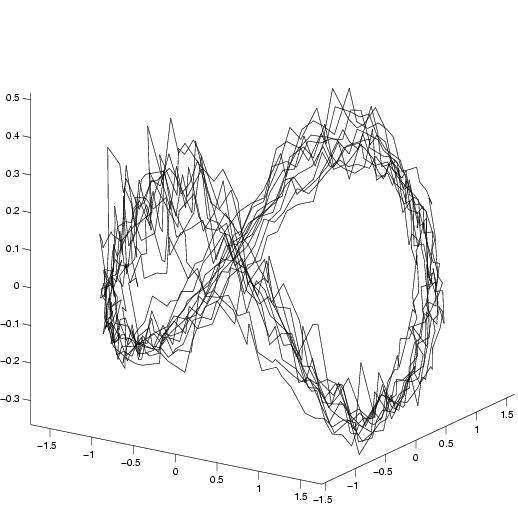
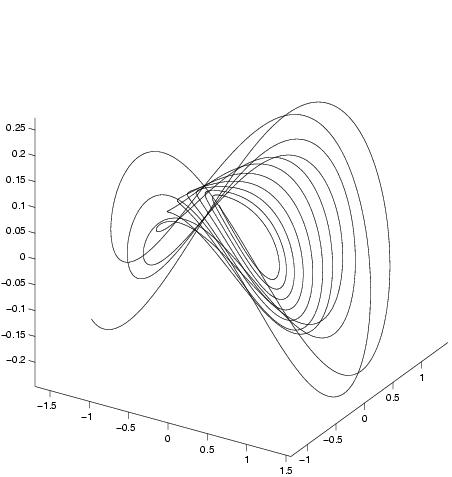
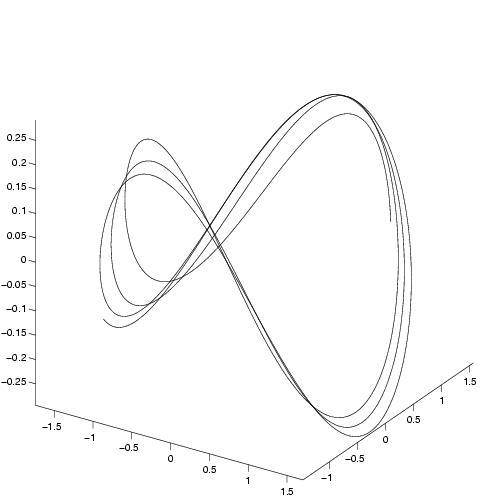
Phase portrait of the first modes:

2D trajectory
3D trajectory
	Observed modes (from PIV)	First estimation	assimilation t=300	assimilation t=1000

The assimilation gives good results for the two first modes, which represent the big structures of the flow. For the following modes, the estimation is acceptable for 300 images. Indeed, as the last modes concern the small fluid structures, their observations are very noisy.

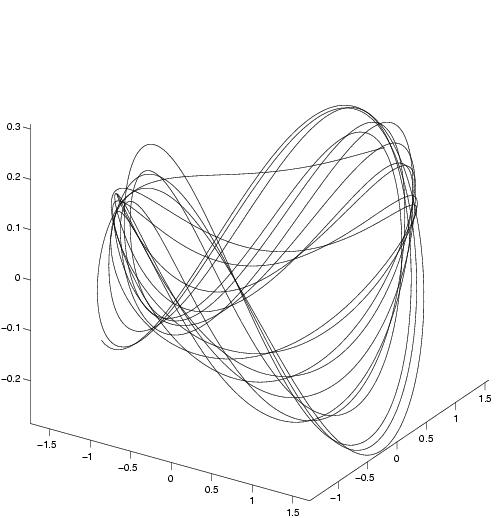
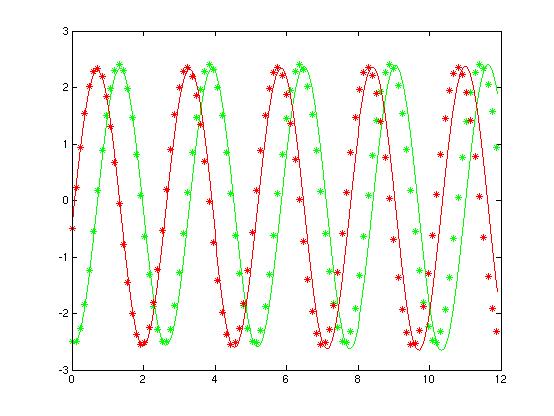
Experience 2: Flow behind a rotating cylinder

2 modes on 800 images

For this experience, the first estimation based on least squares fitting is really bad.

First estimation	Assimilation	New estimation

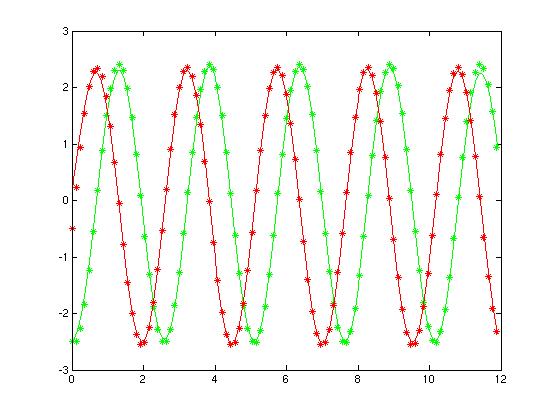
A new least squares fitting is realized on the assimilation results in order to provide new coefficients. They lead to a better estimation from the initial condition.

A new version of the technique also enable to control the coefficient of the LODS through data assimilation concepts, in order to directely estimate the reduced model.

Reference

J. D'adamo, N. Papadakis, E. Memin, G. Artana. Variational assimilation of POD low-order dynamical systems. Accepted for publication in Journal of Turbulence.