The Sigali Tool Box
Overview of the tool
Sigali is a model-checking tool-based which manipulates ILTS:
Implicit Labeled Transition Systems (which can be seen as an equational
representation of an automaton) as intermediate models for discrete event
systems. It offers functionalities for verification of reactive systems and
discrete controller synthesis. It is developed jointly by Espresso and Vertecs.
The techniques used consist in manipulating the system of equations instead of
the sets of solution, which avoids the enumeration of the state space. Each set
of states is uniquely characterized by a polynomial and the operations on sets
can be equivalently performed on the associated polynomials. Therefore, a wide
spectre of properties, such as liveness, invariance, reachability and
attractivity can be checked. Many algorithms for computing predicates states
are also available.
Contact: Hervé Marchand.
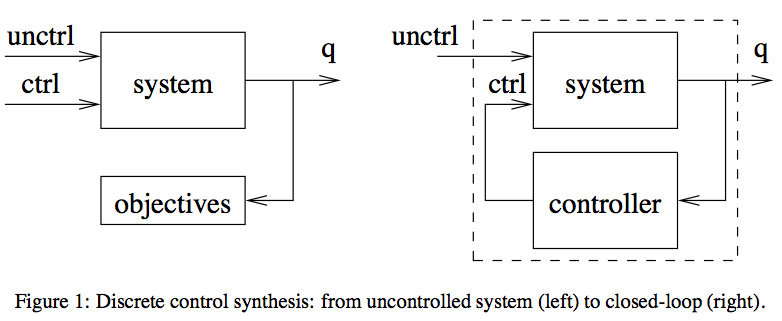
The Controller Synthesis methodology
Control theory of discrete event systems allows to use constructive
methods, that ensure, a priori, required properties on the system behavior. In
this approach, the validation phase is reduced to properties not guaranteed by
the programming process. Starting from a representation of the possible
behaviors of the system(e.g. in the form of a finite state automaton) and the
properties that have to be satisfied by the controlled system, the synthesis
produces directly the constrained automaton, i.e., the one that presents only
those behaviors that satisfy the required properties.
In our framework, The
system is represented by an ILTS while the control of the system is performed
by restricting the controllable input values to values suitable for the control
goal. This restriction is obtained by incorporating new algebraic equations
into the initial system.
Using symbolic methods (based on BDD techniques, avoiding state
space enumeration), The various control objectives for which we are
able to synthesize a controller are the following:
- ``Traditional'' control objectives such that:
- The invariance of a set of states E. Note that if the
property is expressed by means of an observer O, with a sink state
Error, then it is sufficient to perform the synchronous product
between the ILTS modeling the plant and the observer and to
compute a controller that avoids states of the form (q,Error) to
be reachable in this new system.
- the reachability of a set of states from the initial states of the system,
- the attractivity of a set of states E from a set of states F.
- the persistence of a set of states E.
- the reccurence of a set of states E.
- Control objectives expressed as partial order relations over the states
of the system such that:
- the minimally restrictive control (choice of a command such that
the system evolves, at the next instant, into a state where the maximum
number of uncontrollable events is admissible)
- the stabilization of a system (choice of a command such that the
system evolves, at the next instant, into a state with minimal change for the
state variable values)
- the optimal control (minimization of the cost of the trajectories
between a set of initial states and a set of final states)
Sigali Tool Box
Sigali is a tool box that manipulates (sets of) variables and
predicates by means of (predefined) functions using a
Mathematica-based language. Using Sigali, one can create
predicates over a set of variables. There exists functions to
manipulate them (intersection, union, complementary, test of
inclusion, etc). Some functions are used to replace some variables in
a predicate by other predicates. All these operations are extended to
the manipulation of lists of predicates. Sigali also manipulates
cost functions. These are functions that associate to each solution
of a predicate a given integer value. These cost functions can be
build by associating to each variable a given cost according to the
value of the variable.
Starting from the existing functions, it is also possible to define
new functions, allowing, from example, to have libraries of functions
dedicated to controller synthesis, optimal control or verification.
Of course, one can also manipulate ILTS (e.g. to compose them
according to different composition operators). Functions allowing to
compute the successors (resp. predecessors, etc) belongs to the
function kernel of Sigali. They can be further used to implement more
intricate functions as the ones that compute the set of reachable
states, the set of states that can reach a set of states by triggering
uncontrollable events, etc.
For more details regarding Sigali, its syntax and the librairies see the Sigali user manual (pdf)
Sigali front-ends and back-ends
The current implementation
of the method relies on the chain of Figure 2. Centrally, we
use Sigali, which is a tool that performs model-checking,
controller synthesis for logical goals, and optimal controller
synthesis.
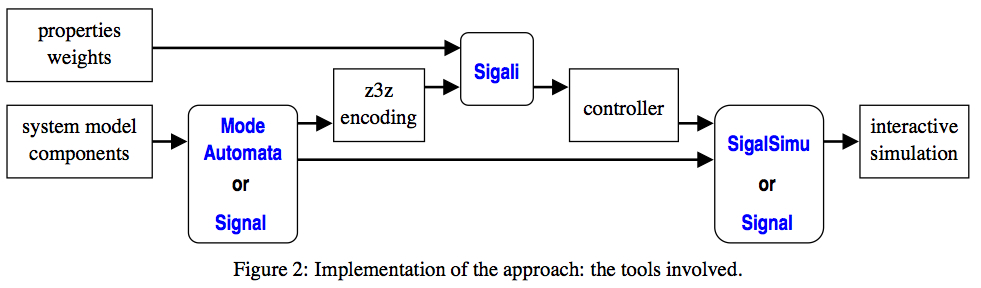
- Sigali is connected with the Polychrony
environment, allowing both the specification of the system in Signal
and the the visualization of the synthesized controller by an interactive
simulation of the controlled system.
Here is a user Signal/Sigali Manual.
- Sigali is now connected with the Matou environment
thus allowing the modeling of reactive systems by means of Mode
Automata. The simulation of the controlled system is also possible.
When the purpose is to control the system, the result of the synthesis
in Sigali is a controller, in the form of a logical relation,
which can be interpreted by a resolver module: for a given state and
uncontrollable inputs, the constraints on controllable signals are
solved, for example in an incremental, interactive way following the
manual valuation of signals. The resolver can be coupled with the
original specification of the uncontrolled system, using either the
Polychrony environment, or the tool SigalSimu in the case of
Mode Automata.
Distribution
Sigali is freely available for non-commercial use.
Note that you will need part of the Polychrony or Matou environment as
front-end in order to specify your systems.
Examples
Sigali has been successfully used to verify or control various
academics or industrial systems (See the list below).
-
Some academic examples (The cat and mouse example & the AGV
example) are explained in [1].
- In [2], the synthesis methodology has been
applied to the incremental design of a power transformer station
controller.
- in [3,4], we have been
interested in the automatic control of systems with multiple tasks,
each with multiple modes, implementing a functionality with
different levels of quality (e.g., computation approximation), and
cost (e.g., computation time, energy) and we made the use of
Sigali in order to control the switching of modes in order to
insure properties like bounding cost while maximizing quality.
-
The same approach was applied to the control of reconfigurations in fault-tolerant systems [5]
Papers
More details concerning Sigali are available in the following papers:
- [1] H. Marchand, P. Bournai, M. Le Borgne, P. Le Guernic, Synthesis of Discrete-Event Controllers based on the Signal Environment, Discrete Event Dynamic System: Theory and Applications, 10(4):325-346, October 2000. (more)

- [2] H. Marchand, M. Samaan, Incremental Design of a Power Transformer Station Controller using Controller Synthesis Methodology, IEEE Transaction on Software Engineering, 26(8):729-741, August 2000. (more)

- [3] H. Marchand, E. Rutten, Managing multi-mode tasks with time cost and quality levels using optimal discrete control synthesis, in 14th Euromicro Conference on Real-Time Systems (ECRTS'02), June 2002. (more)

- [4] E. Rutten, H. Marchand, Task-level programming for control systems using discrete control synthesis, Research Report INRIA, No 4389, February 2002. (more)

- [5] E. Dumitrescu, A. Girault, H. Marchand, E. Rutten, Optimal discrete controller synthesis for the modeling of fault-tolerant distributed systems, in First IFAC Workshop on Dependable Control of Discrete Systems (DCDS'07), Paris, France, June 2007. (more)

- [6] H. Marchand, M. Le Borgne, The Supervisory Control Problem of Discrete Event Systems using polynomial Methods, Research Report Irisa, No 1271, October 1999. (more)