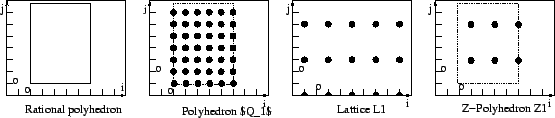
A ![]() -polyhedron can be defined as the image of a polyhedron by an
invertible, integral function. Consider, for instance, the lattice
-polyhedron can be defined as the image of a polyhedron by an
invertible, integral function. Consider, for instance, the lattice
![]() and the polyhedron
and the polyhedron
![]() . Then
. Then
![]() is
a
is
a ![]() -polyhedron (see figure
-polyhedron (see figure ![[*]](crossref.gif) ).
). ![]() can also be expressed as:
can also be expressed as:
 |
As Polylib operates on domains made out of
unions of polyhedra, it is natural to define a similar
object for ![]() -polyhedra. A
-polyhedra. A ![]() -domain is a finite union of intersections
between a domain and a full dimensionnal integral affine lattice.
The set of
-domain is a finite union of intersections
between a domain and a full dimensionnal integral affine lattice.
The set of ![]() -domains is closed under union, intersection,
difference, and image by integral invertible function.
-domains is closed under union, intersection,
difference, and image by integral invertible function.
The image and pre-image by rational functions is also implemented
in Polylib, but the result of the image (or pre-image) is always
intersected with the canonical lattice (![]() ).
See [NRi00] for further detail on this subject.
).
See [NRi00] for further detail on this subject.
From the implementation point of view, a ![]() -polyhedron is represented
internally as the image of a polyhedron by an affine, invertible
mapping. Hence, storing a
-polyhedron is represented
internally as the image of a polyhedron by an affine, invertible
mapping. Hence, storing a ![]() -polyhedron amounts to storing a domain and a
matrix.
-polyhedron amounts to storing a domain and a
matrix.