


Next: Important functions in Lattice.c
Up: Lattices
Previous: Lattices
Contents
Lattice are manipulated in Polylib because they are used in
constructing 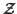 -polyhedra. A subset
-polyhedra. A subset 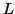 in
in 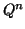 is a lattice if is generated by integral combination of finitely many
vectors:
is a lattice if is generated by integral combination of finitely many
vectors:
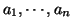 (
(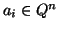 ).
).
If the 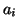 vectors have integral coordinates,
vectors have integral coordinates, 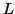 is an integer lattice. If the
is an integer lattice. If the 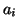 vectors are linearly independent,
they constitute a basis of the lattice. If the vectors
vectors are linearly independent,
they constitute a basis of the lattice. If the vectors
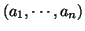 constitute a basis of
constitute a basis of 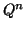 , the
lattice is said to be full dimensional.
, the
lattice is said to be full dimensional.
The affine object corresponding to a lattice is called an affine
lattice. It is constructed by adding the same constant vectors to
all the points of a lattice. For instance, the set
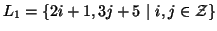 can be interpreted as an affine
lattice: it is the lattice defined by any integral linear
combinations of the vectors
can be interpreted as an affine
lattice: it is the lattice defined by any integral linear
combinations of the vectors 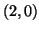 and
and 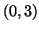 , plus the vector
, plus the vector
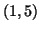
In Polylib, only full-dimensionnal affine integral
lattices are considered. It can easily be proven that an element
of this subset of affine lattices can always be represented by a
non singular integral matrix and an integral vector. For
instance, lattice 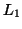 above, will be mathematically represented
by:
above, will be mathematically represented
by:
The data structure used to represent an affine lattice in
Polylib is an affine matrix. For example, lattice 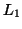 will be represented
in Polylib by the following matrix:
will be represented
in Polylib by the following matrix:
Lattice manipulation naturally leads to an intensive use of the
Hermite normal form (HNF).
Definition 3 (
Hermite normal form)
A matrix
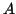
of full row rank is said to be in Hermite normal form (HNF) if it
has the form
![$[B \ 0]$](img71.gif)
where
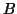
is a non singular, lower triangular,
non negative matrix, in which each row has a unique maximum entry
located on the main diagonal of
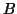
.
Theorem 1
For any rational matrix
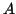
of full row rank, there exists a unique
matrix
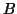
in Hermite normal form and a unimodular matrix
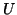
such that
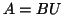
.
Consider the following matrices 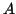 ,
, 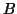 and
and 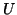 . Then
. Then
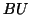 is the Hermite decomposition of
is the Hermite decomposition of 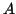 .
.
Proposition 3
(uniqueness of the Hermite normal form)
Let
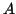
and
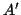
be rational matrices of full row rank, with Hermite
normal forms
![$[B \ 0]$](img71.gif)
and
![$[B' \ 0]$](img77.gif)
, respectively. Then the columns
of
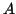
generate the same lattice as those of
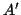
, if and only if
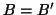
.
In other words, two lattices are equal if and only if their
respective matrices have the same Hermite normal form.
Proposition 4
(lattice canonical form)
Given a full-dimensional linear lattice
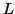
,
there exists a unique representation
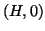
of
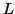
(i.e.
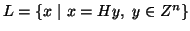
), such that
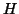
is in Hermite normal form.
Proposition 5
(affine lattice canonical form)
Given a full dimensional affine
lattice
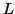
,
there exists a unique representation
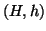
of
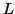
(i.e.
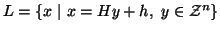
), such that
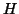
is
in Hermite normal form and
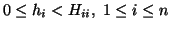
.
For instance, consider the following lattice 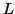 :
:
its unique
canonical form is
Polylib can also handle unions of (affine
integral full dimensionnal) lattices. This provides a set of
objects which is closed
under union, intersection, image by invertible integral functions
(see [NRi00]).
For instance, consider the following lattice 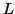 :
:
its unique normal form is



Next: Important functions in Lattice.c
Up: Lattices
Previous: Lattices
Contents
Sorin Olaru
2002-04-24
![]() vectors have integral coordinates,
vectors have integral coordinates, ![]() is an integer lattice. If the
is an integer lattice. If the ![]() vectors are linearly independent,
they constitute a basis of the lattice. If the vectors
vectors are linearly independent,
they constitute a basis of the lattice. If the vectors
![]() constitute a basis of
constitute a basis of ![]() , the
lattice is said to be full dimensional.
, the
lattice is said to be full dimensional.
![]() can be interpreted as an affine
lattice: it is the lattice defined by any integral linear
combinations of the vectors
can be interpreted as an affine
lattice: it is the lattice defined by any integral linear
combinations of the vectors ![]() and
and ![]() , plus the vector
, plus the vector
![]()
![]() above, will be mathematically represented
by:
above, will be mathematically represented
by:
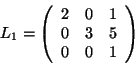
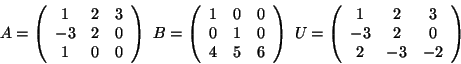
![]() :
:
![]() :
: