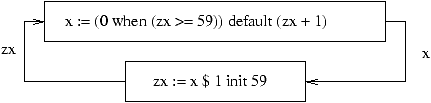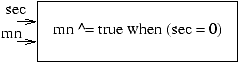Polychrony
A short introduction to SIGNAL
A more complete description is provided in documentation items.
Read also introductory papers.
1 Context
An embedded application cooperates with its environment to achieve a mission that may be real-time and critical. These interactions result from communications via a definite set of input/output devices that we call ports. An output port of a system (respectively, of the environment) can be connected to one or more input ports of the environment (respectively, of the system).If two ports are connected (as in figure 1 for application left output, env1 input, env2 upper input) they hold the same sequence of values. In a physical time view, the elementary values are in general not simultaneously held by the physical ports (such a physical link may even not exist). Thus time is abstracted in Signal as a virtual discrete time domain (analog computing is out of the scope of Signal). AD/DA converters are assumed to belong to the environment (nevertheless sampling rates as well as front events can be described in Signal).
2 Flows
A named variable (an identifier) is associated with each port. Thus a Signal identifier denotes an elementary flow: the sequence of values that the system (or its environment) produces. Function call occurrences in a program, fronts of a Boolean signal, samples in a continuous signal, click events on a mouse, etc., are examples of elementary flows. A type notation is associated with an elementary flow; it is the type of its elements. For instance if an identifier mn holds the new minute value at each minute change, and a second identifier sec holds the new second value at each second change, mn and sec both denote the following sequence of integers: 0 1 иии 20 иии 59 0 1 иии
This sequence is held by x in the following conjunction of Signal equations
(figure 2), which is a way of writing that x is
equal to 0 when its previous value (zx) is equal (greater than or equal)
to 59, and to its previous value incremented by 1 otherwise:
Usually, a system has several ports. It may then occur that two ports hold values at different instants. For instance mn changes occur every 60 sec: when sec holds 0. When sec holds another value, there is no minute change and then no value is associated with mn: mn is said to be absent. Such a ``clock'' synchronization is written in Signal as (figure 3):
We name flow a set of coordinated elementary flows: a flow can be seen as a sequence of configurations or events as for instance the sequence:
(mn,0),(sec,0) , (sec,1) , ..., (sec,59) , (mn,1),(sec,0) , ...
in figure (4).
Such a generalized flow denotes not only sequences of values associated with variables but also synchronization constraints between the elements of the sequences.
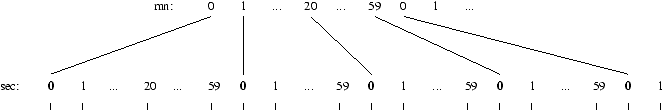
Figure 4: _|_ in time line
3 Clocks
In the coordinated evolution of both mn and sec, the semantic notation _|_ is used to represent the absence of mn occurrence, as shown in figure 5.One can associate with an elementary flow mn an elementary Boolean flow which is true if and only if mn is present. Such a flow is said to be a clock for mn. Among clocks present(mn) and event(mn) are distinguished (figure 5). The clock present(mn) is defined as in Lustre, event(mn) is the minimal clock of mn: elements of this clock are true or absent. The minimal clock event(mn) is a pure flow close to pure signals used in imperative languages such as Esterel or Statecharts. A Boolean clock may itself be associated with a clock flow, but in contrast with Esterel and Lustre there is no universal clock such as tick or true in Signal.
event(mn): T _|_ иии _|_ иии _|_ T _|_ иии _|_ T _|_ иии _|_ T _|_ иии _|_ T _|_ иии present(mn): T F иии F иии F T F иии F T F иии F T F иии F T F иии mn: 0 _|_ иии _|_ иии _|_ 1 _|_ иии _|_ 20 _|_ иии _|_ 59 _|_ иии _|_ 0 _|_ иии sec: 0 1 иии 20 иии 59 0 1 иии 59 0 1 иии 59 0 1 иии 59 0 1 иии | | | | | | | | | | | | | | |
Figure 5: Clocks in time line
4 Processes
In Signal, to specify the behavior of an embedded system, the designer writes a process as an invariant relation on its external flows rather than an explicit sequencing of actions. Relations are incrementally built as composition of subrelations; elementary relations are equations on signal expressions, specialization of generic relations (user defined processes) and abstractions of external components. Actual serialisation of flow sample evaluation results mainly from causality, data dependence and explicit ordering of external actions.4.1 Composition
Composition of two processes P1 and P2 is written P1 | P2. Its result is the conjunction of their respective constraints: the behavior of P1 | P2 is the set of flows such that, at each instant, both P1 and P2 agree on the value (and the presence status) of their common variables. For instance the time counter (figure 2) has two processes, one for each box. The first (upper box) process P1: x := (0 when (zx >= 59)) default (zx + 1) has one (free) input zx, and one output x; it allows the configuration (e1) of an event where, for example, zx=-10 and x=-9. The second (lower box) process P2: zx := x $ 1 init 59 has one (free) input x, and one output zx; it allows the configuration (e2) of an event where, for example, zx=90 (when the previous value of x is 90) and x=30. But the inital value of zx is positive (P2), thus x is positive forever and then (e1) is not a possible configuration of P1 | P2; in the same way, (e2), allowed in P2 is not possible in P1 | P2.4.2 Equations
An elementary process is built as an equation on flow expressions. Some operators used in these expressions need to have either all their arguments present, or all their arguments absent: we call them monochronous operators (they handle a single clock). We use the term polychronous for the other operators: they can handle several clocks. By extension processes are said to be monochronous or polychronous.Function iteration:
x := f(x_1,...,x_n)For a usual function f defined with n arguments, the Signal process x := f(x_1,...,x_n) is the monochronous process such that at every instant t, xt is equal to f(x_1t,...,x_nt).
These monochonous processes are built on a large set of operators including usual Boolean, integer, real, matrix, etc., operators.
All domains of values are supposed to provide a monochronous equality test operator == such that x == y is true when x and y are equal. For a flow x, its pure clock x is true if and only if x is present: thus x is equivalent to x == x.
Delay:
zx := x $ 1 init vis the monochronous process such that at every instant t, if x is present, zxt is equal to:
- v if t is the first instant at which x is present,
- xprev(t) otherwise (where prev(t) is the latest instant before t at which x is present).
zx := x $ n init V
where n is a positive integer constant, and V a vector of length n.
The Signal language does not provide constant flows associated with an implicit clock; nevertheless one can define a signal x which holds a constant value v, as:
x := x $ 1 init v
x := v
is a shortcut for this definition.
Flow extraction:
x := y when cis the polychronous process such that at every instant:
- if c is present and holds the value true then x and y are equal (or both absent),
- if c is absent or holds the value false then x is absent.
Flow fusion:
x := y default zis the polychronous process such that at every instant:
- if y is present then x and y are equal,
- if y is absent then x and z are equal (or are both absent).
x := y when (y >= 0) default (-y)
returns in x the absolute value of y;
x := y when (y >= 0) default x
partially defines x as being the value of y when it is present and positive; otherwise, x is no more defined. If x definition is not completed elsewhere, then the value of x is undetermined when y is absent or negative. This partial definition is written as:
x ::= y when (y >= 0)
4.3 User defined processes
Processes can be abstracted as user defined models of processes that can be further instantiated and used as processes in a given context. For example, the time counter (figure 2) can be declared as follows:
process time_counter =
{integer max_value;}
( ?
! integer x;
)
(| x := (0 when (zx >= max_value)) default (zx + 1)
| zx := x $1 init max_value
|)
where
integer zx;
end;
The process model time_counter has no input (no signal is specified
behind the input symbol ``?''; it has one output signal (specified
behind the output symbol ``!'') of type integer: x.
The signal zx is defined as a local variable. The max value of the counter
is declared here as a formal parameter of the process model (between brace brackets).The process model time_counter can be used as follows, for instance, to define the signals mn and sec, synchronized by the equation of figure 3 (simplified form):
(| sec := time_counter{59}()
| mn := time_counter{59}()
| mn ^= when (sec = 0)
|)
This document was translated from LATEX by HEVEA and HACHA.