This page is divided into the following sections:
To measure the complexity of the learning task, and to ensure that the training data meets requirement 1 and requirement 2 , a model of the learning task was constructed. This involved the creation of a new grammatical inference algorithm that we will call the BruteForceLearner algorithm. This algorithm constructs a huge model space using the training example and attempts to find the most general grammar consistent with both positive and negative data. In this section it will be proven that this algorithm can be used to identify any context-free grammar in the limit from positive and negative data (although it does so in exponential time). DDD
Computational linguistics use the terms words, sentences and lexicons while formal language theorists tend to talk about letters, words and alphabets for the same items so we will begin by defining the terms that we will use in this document.
Definition. A sentence is comprised of a concatenation of symbols known as words . A language defines a set of sentences. The lexicon of a language defines the set of words contained in the language.
Definition. A grammar is unambiguous if for each sentence there is only one possible derivation tree.
Definition. A language is deterministic if there exists a deterministic pushdown automaton that can recognise the language.
If a language is deterministic then there exists an unambiguous grammar that can recognise the language. However, not all unambiguous grammars represent deterministic languages.
In the identification in the limit paradigm (Gold 1967 ) the learner is presented with a set of training sentences generated from a target grammar, one sentence at a time. After receiving a sentence the learner may update their model of the language, so that it conforms to the new training example. The process continues on forever, but in such a way that every string in the language is presented to the learner at least once. If after some finite time the learner’s model of the language does not change, and that model is identical to the target language, then the language has been identified in the limit.
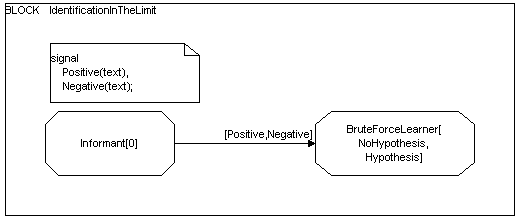
In this document we will consider a variation of the identification in the limit scenario where negative sentences are also presented to the learner. In this model the informant presents negative data as well as positive data. Both the positive and negative examples are randomly presented to the learner but with the following conditions.
Figure 1 below shows an SDL block diagram describing the process. In this definition positive examples are sent in messages of type “Positive” while negative examples are sent in messages of type “Negative”.
Figure 1 SDL Block Diagram showing the Identification In the Limit Scenario with Arbitrary Informant
We will now introduce a grammatical inference algorithm that uses a brute force search technique to infer a grammar. This algorithm is described using SDL in Figure 2 below .
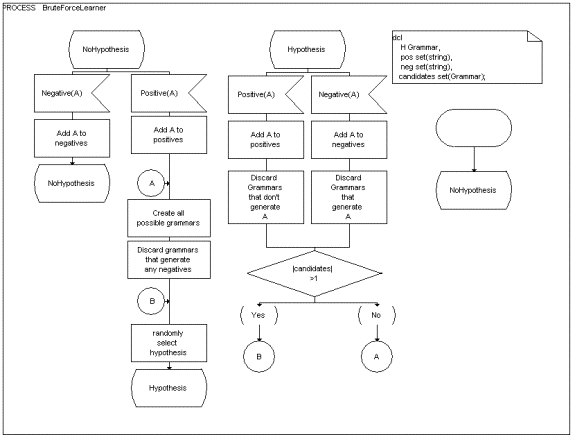
Figure 2 SDL Process Diagram describing the BruteForceLearner algorithm
The BruteForceLearner algorithm has the local variables as shown in Table 1 below .
Table 1 Local Variables used in the BruteForceLearner Algorithm
|
Variable Name |
Purpose |
|
H |
The hypothesis grammar |
|
Pos |
A set of observed positive strings |
|
neg |
A set of observed negative strings |
|
Candidates |
A set of candidate grammars. |
The algorithm has two states “NoHypothesis” and “Hypothesis”. The algorithm begins in state “No Hypothesis”. The value of H is initially set to the grammar that generates exactly the empty string.
1. In the state “NoHypothesis” if the algorithm observes a negative example (receives a “Negative” message) then the string contained in the message is added to “neg”.
2. In the state “NoHypothesis” if the algorithm observes a positive example the algorithm calls the function CreateAllPossibleGrammars . This clears the variable candidates and then stores into it a set of hypothetical grammars using the contents of the variable pos .
The algorithm then calls the function Discard that removes from candidates any grammars that can generate any sentences contained in neg .
The algorithm then randomly selects a grammar from the set candidates using the function BestMatch .
3. In the state “Hypothesis” if the algorithm observes a positive example it adds the sentence to its set of positive examples ( pos ). It then deletes from candidates any grammar that cannot generate the newly observed positive sentence. If the set candidates is not empty an element is then randomly selected from it to be the hypothesis grammar. If the set candidates is empty then all positive grammars that could generate the positive examples are created (using the function CreateAllPossibleGrammars) and placed into the set candidates . All grammars that generate any negative examples are then removed (using the function Discard ), and one grammar is randomly selected from the set candidates to become the hypothesis grammar (using the function BestMatch ).
4. In the state “Hypothesis” if the algorithm observes a negative example the algorithm adds the sentence to its set of negative examples ( neg ). It then checks to see if this negative example is consistent with it’s current hypothesis (H). If the sentence is not consistent with the hypothesis then all grammars in the set candidates that are inconsistent with neg are then removed from candidates. This is achieved using the function Discard . If the set candidates is empty then all possible grammars that could generate the positive examples are created using the function CreateAllPossibleGrammars. This set is then reduced using the function Discard and one grammar is randomly selected using the function BestMatch .
We will now define the most important function CreateAllPossibleGrammars.
Definition.
A context-free grammars is in Chomsky Normal Form (CNF) if all rules in the grammar are in one of the following three forms
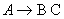
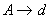
Where
S is the start symbol
is a symbol representing the empty string
A, B and C represent a non-terminal and
d is a terminal.
Definition. The function CreateAllPossibleGrammars (O) is defined to be a function that
· takes as its argument a set of positive strings O and
· creates a set of grammars X such that
o if there exists a set of labelled derivation trees D that can be assigned to O by a grammar in Chomsky Normal Form then
o there is a grammar contained in X that can generate a set of labelled derivation trees E such that E is identical to D up to the naming of non-terminals.
There exists an implementation of the function CreateAllPossibleGrammars (O).
Proof Sketch of Theorem 1 (Proof by Construction)
Given any sentence generated from a grammar in Chomsky normal form there is a finite number of unlabelled derivation trees that can be assigned to that sentence. The number of derivation trees is described by the Catalan numbers . (Aho and Ullman 1972 ;Weisstein 2001 ). Each one of these derivation trees has a maximum number of non-terminals that can be referenced by that derivation tree (Hopcroft, Motwani et al. 2001 ). Using these two numbers, the maximum number of non-terminals that can be referenced by any set of labelled derivation trees of the positive examples can be calculated. Using this number a set of non-terminals can be defined. Using the set of non-terminals, all possible sets of labelled derivation trees that could be assigned to the positive sentences can be calculated. Q.E.D.
Let G = { N, S , P
,S) be a context-free grammar. Let D be a set
of labelled derivation trees such that for each rule P 
P there is at least one sentence in O derived
using P.
Claim: G can be reconstructed from O
Proof by Construction.
For all labelled derivation trees the rules used to construct those trees can be determined. Because all rules are represented in O, the union of the set of rules reconstructed from each element of O is exactly P .
For any context-free grammar G 1 there is a set of sentences that can be generated from G 1 such that when presented to the BruteForceLearner algorithm, the set candidates contains at least one grammar G 2 such that L(G 1 ) = L(G 2 ).
Proof by Construction
All context-free grammars can be converted to a grammar in CNF.
(Chomsky 1956 ). Convert G
1
to the a grammar G
3
= { N
3
, S
3
, P
3
,S) in CNF. Generate a set of sentences O
3
from G
3
such that for each rule P 
P
3
in G
3
there is at least one sentence in O
3
derived using P.
For each O 
O
3
According to Theorem 1 when presented with O the function
GenerateAllPossibleGrammars
generates creates a set of grammars X such that there is
at least one grammar G
2
X that assigns the same labelled derivation to O as
that assigned by G
3
(up to the naming of non-terminals). Because for each rule P
P
3
in G
3
there is at least one sentence in O
3
derived using P, according to Lemma 1 there is at least
one grammar G
2
X that is identical to G
3
up to the naming of non-terminals.
Lemma 2
For any context-free grammar G 1 there is a set of positive and negative examples O that can be generated from G 1 such that when presented to the BruteForceLearner algorithm, the algorithm generates a hypothesis G 2 such that L(G 1 ) = L(G 2 ).
Proof by Construction
Convert G 1 to the grammar G 3 = { N 3 , S 3 , P 3 ,S) in CNF.
Construct the set O = O
1
O
2
Such that
The set O 1 is constructed as follows;
Generate a set of sentences O
3
from G
3
such that for each rule P 
P
3
in G
3
there is at least one sentence in O
3
derived using P.
Construct a random set of sentences O 4 such that |O 4 | > = 0 and all positive examples in O 4 can be generated by G 1 and no negative examples in O 4 can be generated by G 1 .
Let O
1
= O
3
O
4
.
According to Theorem 2 when presented with O
1
the function g
enerateAllPossibleGrammars
creates a set of grammars
candidates
such that there is at least one grammar G
2
candidates
, such that L(G
1
) = L(G
2
) = L(G
3
). At this point G
2
will never be removed from
candidates
and no new grammars will be added
candidates.
Consider the set H = { H
i
: H
i
candidates
, L(H
i
) = L(G
1
) } i.e. the set of all bad grammars contained in
the set
candidates.
Because |
candidates
| is finite, |H| is also finite. We will now demonstrate
that if O
1
is known the set O
2
can be constructed so that for each H
i
H one sentence (either negative or positive) can be added
to O
2
, such that on presentation of O
2
after O
1
the algorithm
BruteForceLearner
will remove all elements of H
from the set
candidates
.
The set O 2 is constructed as follows
Let P = all positive examples in O 1
Let Q = all negative examples in O 1
Let H = Discard (G enerateAllPossibleGrammars ( P), Q)
Note that H = candidates after the presentation of the set O 1 .
For all grammars H
i
H either
L(G
1
) Case 1. L(H i ) = L(G 1 )
Nothing needs to be added to O 2 as a result of H i .
Case 2. L(H
i
) 
L(G
1
)
In this case one of the two following cases is true
L(G
1
)
Case 2.1 L(H i ) Ě L(G 1 )
In this case by definition there is at least sentence O
such that O 
L(G
1
) and O 
L(H
i
).
Add the positive example O to the set O 2.
On receipt of O the algorithm BruteForceLearner will remove H i from candidates.
Case 2.2 L(H
i
) 
L(G
1
)
In this case by definition there is at least sentence O
such that O 
L(H
i
) and O 
L(G
1
).
Add the negative example O to the set O 2.
On receipt of O the algorithm BruteForceLearner will remove H i from candidates.
All context-free grammars can be identified in the limit with the BruteForceAlgorithm when presented with both positive and negative data.
Proof.
According to Theorem 2 for all context-free grammars a set of example sentences O 1 can be constructed that forces the algorithm BruteForceLearner to include G 1 in the set candidates . If O 1 is presented to the algorithm with any combination of zero or more other positive or negative examples then the algorithm BruteForceLearner will still include G 1 in the set candidates. Because in the identification in the limit scenario the presentation includes all possible sentences in L(G 1 ) at least once, so there is guaranteed to be a finite time after which the set candidates will include a grammar G 2 such that L(G 1 ) = L(G 2 ). This grammar will never be subsequently removed from candidates .
According to Theorem 2 for any set O 1 a set O 2 can be constructed such that when any superset of O 2 is observed by the algorithm BruteForceLearner it will eliminate all incorrect hypotheses. Because in the identification in the limit scenario the presentation includes all possible sentences in L(G 1 ) (marked as positive examples) at least once and all possible sentences not in L(G 1 ) (marked as negative examples) at least once there will be a finite point in time at which the algorithm has correctly identified the target language. After this point all positive examples will be consistent with the hypothesis and all negative examples will be consistent with the hypothesis. Q.E.D.
In this section we will prove the following theorem.
Given any set of sentences O , where at least one sentence has length longer than 2 the maximum number of grammars that need to be constructed by the BruteForceLearner algorithm to ensure that the grammar is identified in the limit is at most described by
Equation 1 , w here T(O) is the number of terminals in O.
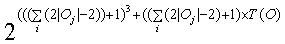
To prove this theorem we will begin by proving that although not all context-free grammars are unambiguous, all context-free grammars can be put into a form, where there exists for each rule P, at least one sentence w such that all derivations of w use P. Knowing this enables the BruteForceLearner to consider only a single derivation for each parse tree. This restriction significantly reduces the number of non-terminals that need to be considered. We will then prove that calculating all possible derivation trees for all sentences is an overly complicated method of constructing grammars. An alternative is to calculate the maximum number of non-terminals required to represent all possible derivation trees, and then construct all possible grammars that have at most that many non-terminals. This alternative method of constructing all possible grammars, while still exponential is significantly less complicated and quicker.
We will now prove that considering only a single derivation for each sentence is sufficient to identify the target grammar, even if the target language cannot be represented by an unambiguous grammar. To do this we will need to define the term minimal form.
Definition.
A context-free grammar G = { N, S , P
,S} is in a
minimal form
if for all P 
P there exists a
w
L(G),
w
L( { N, S , P - {P})
,S}. Informally a grammar is in minimal form if the removal
of any rule would reduce the language generated by the grammar.
Any context-free grammar can be put into a minimal form, simply by deleting redundant rules.
If in an implementation of the algorithm BruteForceLearner the function CreateAllPossibleGrammars considers only a single derivation for each sentence in the training set then the algorithm BruteForceLearner will still identify the language in the limit using an arbitrary informant.
Proof by Construction.
Firstly convert G 1 to CNF. If G 1 is not in a minimal form convert it to a minimal form. According to Lemma 3 this is possible for all context-free grammars.
From the definition of a minimal form it is known that
for each rule P 
P there is at least one sentence O
P
that could not be generated by the grammar if P was
removed. This is known because if this was not the case
then when P was removed then O
P
could still be derived. This would be a contradiction of the
definition of minimal form. This implies that all derivations of O
P
will include a node that references P.
For each rule P add O P to the characteristic set O 3 .
Because all derivations of O P use P only one of these derivations need be considered by the BruteForceLearner for the algorithm to reconstruct P.
When presented with a set of positive training examples O the BruteForceLearner need only construct grammars with at most the number of non-terminals described by
Equation 2 below .
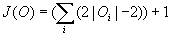
Proof.
Firstly according to Theorem 5 the BruteForceLearner algorithm need only construct a single derivation tree for each sentence.
According to Hopcroft, Motwani et al. (2001 ) in any CNF grammar all parse trees for strings of length n have 2 n -1 interior nodes [1] .
One of the non-terminals is known to be the start symbols (S) therefore the number of non-terminals other than the start symbol is 2 n -2.
When considering all possible labelled derivations trees, All possibilities need be considered from the most specific grammar (that can generate only the training examples) to the most general grammar (that can generate any sentence of any length using the lexicon of the language.)
The most specific grammar can be represented by a grammar, where for each node of all derivation trees, that non-terminal is not used in any derivation tree. There is no grammar that is more specific than that grammar. For that scenario each derivation contributes 2n-2 non-terminals other than the start symbol. If all sentences are considered the maximum number of non-terminals that need to be considered is described by Equation 2 . All possible grammars that are more general than this grammar enable at least one non-terminal of the derivation tree to generate additional sequences. In that case at least one of the non-terminals in the derivation is common with another non-terminal in either the same derivation or another non-terminal of a derivation of another sentence.
We will begin by defining an implementation of CreateAllPossibleGrammars that does calculate all possible grammars. We will then show that before the algorithm has constructed all possible derivation trees for a single sentence, the algorithm has constructed all possible grammars that can be constructed using the given number of maximum non-terminals. This implies that the easier task is just to calculate the number of maximum non-terminals (as defined by Equation 2 ) and then calculate all possible grammars that can be constructed using the given number of maximum non-terminals. Once this has been proven the proof of Theorem 4 is straightforward.
|
Function CreateAllPossibleGrammars(O) Inputs: O A set of text strings Local Variables candidates A set of context-free grammars in CNF. nterms An array non-terminal names utrees An array of unlabelled derivation trees ltrees A set of labelled derivation trees ctrees A set of labelled derivation trees tsets An associative array of sets of labelled derivation trees indexed by a text string dsets A set of set of labelled derivation trees iset A set of labelled derivation trees g A context-free grammar in CNF Outputs A set of context-free grammars in CNF. { // set N to be the maximum number of nonterminals that // could exist in any element of candidates N = max_num_terms(O); // create N unique nonterminal names nterms = create_nterms(N); //iterate through the list of positive examples for(i = 0,i<|O|,i++){ // Given O[I] create all possible unlabelled derivation trees //if the target grammar is in CNF. utrees = create_utrees(O[i]); //Calculate all possible labelled derivation trees given utree //and nterms ltrees = label_utrees(utrees,nterms); // Calculate all possible combinations of 1 or more elements from ltrees // i.e. {{ ltrees[0] } ,{ ltrees[1]}, {ltrees[0], ltrees[1]} ... } ctrees = all_combinations(ltrees) // store these combinations; tsets[O] = ctrees; } // calculate a set of candidate sets of labelled derivation trees dsets = all_combinations_combinations(tsets,O); for(i = 0;i<|dsets\;i++){ iset = dset[i]; g = grammar_from_derivations(iset); add_grammar(g,candidates); } return candidates; } |
Figure 3 The function CreateAllPossibleGrammars described in Javascript.
When presented with a positive set of training examples, the algorithm BruteForceLearner does not need to construct all possible labelled derivation trees of all possible examples to construct all possible grammars. Instead it need only calculate the maximum number of non-terminals, and then construct all possible grammars that could be constructed that contain at most that many non-terminals.
Proof
The algorithm CreateAllPossibleGrammars shown in Figure 3 above calculates a set of grammars consistent with the Theorem 1 using the technique defined in the proof of Theorem 1 .
Consider the case where all possible labellings of the first unlabelled derivation tree of a sentence of length > 1 are to be calculated. At this point the algorithm CreateAllPossibleGrammars encounters a terminal node of a derivation tree.
From the definition of Chomsky Normal Form it is known that this node will be generated from a rule of the form
A -> b
Where b is a single terminal.
The symbol b is known but A can be set to any possible non-terminal.
By the time all sentences have been considered, all possible terminal rules of the form A -> b have been considered where A can be any non-terminal from the set of possible non-terminals and b can be any terminal.
Therefore all possible rules of the form A -> b have been considered.
While calculating all possible labellings of the first unlabelled derivation tree of length > 2, the algorithm CreateAllPossibleGrammars encounters a node with no terminal symbols.
From the definition of Chomsky Normal Form it is known that this node will be generated from a rule of the form
A -> B C
Where B and C are single non-terminals.
A, B and C can be set to any possible non-terminal.
Therefore after all possible labellings of this single node is considered all possible rules of the form A -> B C have been considered.
Q.E.D
Proof of Theorem 4 .
According to Theorem 5 the BruteForceLearner algorithm need only construct a single derivation tree for each sentence. In this case according to Lemma 4 the maximum number of non-terminals is described by Equation 2 . According to Lemma 5 the BruteForceLearner algorithm need only calculate the maximum number of non-terminals, and then construct all possible grammars that could be constructed that contain at most that many non-terminals.
Let O be the set of positive training examples. Let T(O) be the number of terminal symbols in O.
The maximum number of rules of the A -> b that
can exist is defined by the equation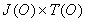 
.
The maximum number of rules of the “A-> B C ”
that can exist is defined by the equation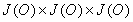 
.
Therefore the maximum number of rules that can exist is defined
by the equation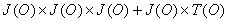 
.
The total number of grammars that can exist can be calculated by considering all possible combinations of each rule either being present or not being present. This defined by the following equation.
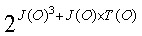
If Equation 2 is substituted into this equation the resulting equation is
.
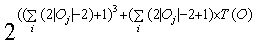Q.E.D.
According to Lemma 6 for any context-free grammar G 1 there is a set of positive and negative examples O that can be generated from G 1 such that when presented to the BruteForceLearner algorithm, the algorithm generates a hypothesis G 2 such that L(G 1 ) = L(G 2 ). The proof of this lemma was a proof by construction, and thus we have already identified a mechanism for generating a training set.
Calculating a set of negative examples using the technique described in the proof of lemma 7 however requires the execution of the function CreateAllPossibleGrammars. Equation 1 describes the number of possible grammars that would exist in the resulting grammars that would be returned. Lets assume that the running time of CreateAllPossibleGrammarsComplete is linear with respect to the number of grammars it generates. If we select a small enough grammar to enable this calculation to be computable in reasonable time, so as to ensure sufficient negative data is available for contestants, we would unfortunately have made the learning task too simple.
For that reason an alternative technique was used to construct the training sets for the Omphalos competition;
The number of training examples was selected to be between 10 and 20 times as large as the characteristic set.
Aho, A. V. and J. D. Ullman (1972). The theory of parsing, translation, and compiling . Englewood Cliffs, N.J., Prentice-Hall.
Chomsky, N. (1956). " Three models for the description of language." IRE transactions on Information Theory 2 : 113-124.
Gold, E. M. (1967). "Grammar identification in the limit." Information and Control 10 (5): 447-474.
Hopcroft, J. E., R. Motwani, et al. (2001). Introduction to automata theory, languages, and computation . Boston, Addison-Wesley.
Weisstein, E. W. (2001). Eric Weisstein's world of mathematics, Wolfram Research, Inc. http://mathworld.wolfram.com
[1] The following table gives some examples of Equation 2 .
|
Length of Sentence (n) |
Number of Bracket Pairs (b(n)) |
Example |
|
1 |
1 |
(S a) |
|
2 |
3 |
(S a b) |
|
3 |
5 |
(S (N 2 (N 3 a) (N 4 b)) (N 5 c)) |
|
4 |
7 |
(S (N 2 (N 3 q) (N 4 b)) (N 5 (N 6 c) (N 7 d))) |
Omphalos is being organized and administered by:
Brad Starkie , François Coste and Menno van Zaanen
You can contact them for comments and complaints at omphalos@irisa.fr
